下記の回路に流れる電流を網目電流法を用いて答えよ。
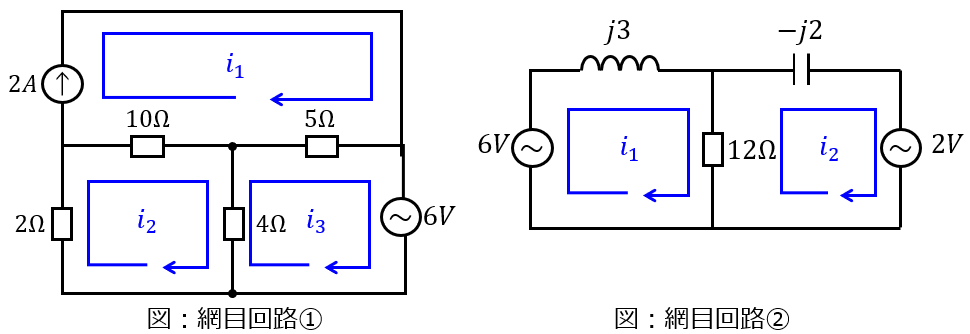
(1)電流源を持つ網目回路。電流変数\(i_{1},i_{2},i_{3}\)
(2)リアクタンス成分を持つ回路と抵抗Rに流れる電流\(i_{R}\)
網目電流法とは
平面グラフにおける網目(メッシュ)毎に電流変数\(I_{i}\)を設定。回路方程式を用いて各網目の電流変数を求める方法を言います。
平面グラフとは、与えられた電気回路が平面上で交差しないものを言います。もし、枝が重なる場合は節点として存在しなければなりません。
なお、ある区間と区間を合わせた複数のメッシュで構成されている領域を一つの電流変数として表すことはできません。
枝電流法との違い
網目電流法は、枝電流法と比較して
- 電流変数の数が少ない。(計算時間:小)
- 立てた回路方程式同士の線形独立性を確認しなくて良い。

1.について、単純に閉路1つを作るためには枝が3本必要です。そのため、枝電流法の場合は3つ変数が必要ですが、網目の場合は1つで済みます。これが全ての網目についてもいえるので、使用する電流変数の数を格段に減らせます。
2.について、枝電流法で電流源を接続する場合を考えます。この場合、節点がn個あればn-1個までしか電流則で線形独立になる式が立てられません。このように、枝電流法の場合、線形独立性に気を付けて立式していく必要がありますが、網目電流法の場合、閉路数の分だけ機械的に立式できます。
網目電流法の使用方法
基本的に、閉路一つごとに回路方程式(電圧則)を立てていけば良いです。ただし、ある素子に流れる電流が、隣の閉路で設定した電流の影響を受ける場合は、その分を考慮して立式する必要があります。
また、電流源が存在する閉路の場合は、その閉路で設定した電流変数は電流源の値に等しくなります。
解答例
(1)電流源付きの網目回路
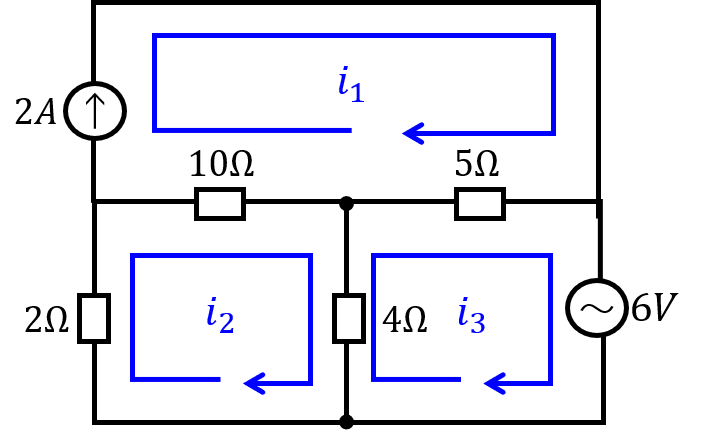
\(I_{1},I_{2},I_{3}\)の回路方程式は
\begin{cases}I_{1}=2 \\ 0=4(I_{2}+I_{c})+10(I_{2}-I_{1})+2I_{2} \\ 6=4(I_{2}+I_{3})+5(I_{3}+I_{1})\end{cases}
上式の\(I_{1}=2\)を第二式、第三式に代入し
\begin{cases}0=16I_{2}+4I_{3}-20 \\ 6=4I_{2}+9I_{3}+10\end{cases}
これを解くと
\begin{cases}I_{2}=\dfrac{49}{32} \\ I_{3}=-\dfrac{9}{8}\end{cases}
(2)リアクタンス付きの網目回路
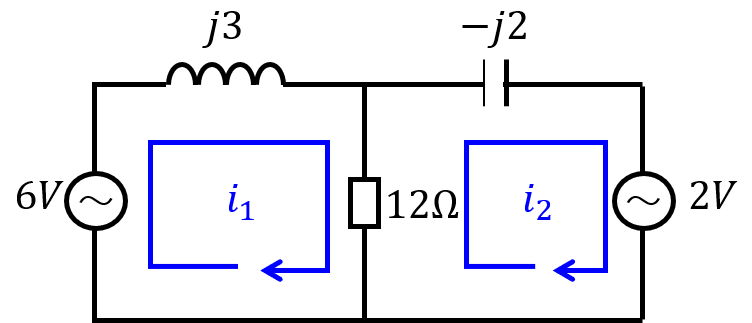
回路方程式は
\begin{cases}6=(12+j3)I_{1}+12I_{2} \\ 2=12I_{1}+(12-j2)I_{2} \end{cases}
これを解ける形に変形する。第1式から第2式を引き算し、\(4=j3I_{1}+j2I_{2}\)。第二式を連立し
\begin{cases}j16=-12I_{1}-8I_{2} \\ 2=12I_{1}+(12-j2)I_{2} \end{cases}
\begin{aligned}I_{2}=-1.2+j3.4\end{aligned}
これを第一式に代入すると
\begin{aligned}12I_{1}&=-j16-8(-1.2+j3.4) \\ I_{1}&=0.8-j3.6\end{aligned}
抵抗Rに流れる電流\(I_{R}\)は、\(I_{1},I_{2}\)の足し合わせなので
\begin{aligned}I_{R}=-0.4-j0.2\end{aligned}
最後に
院試では、基本的に枝電流法で解くことをオススメします。ただし、回路のメッシュが多いときは閉路電流法で解くことも選択肢に入るかもしれません。


