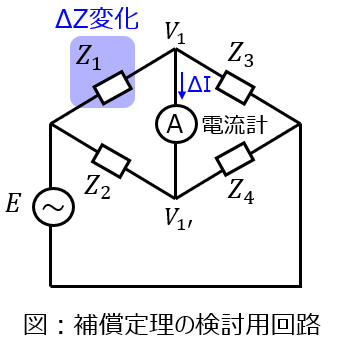
下記の回路が平衡状態になっているとする。\(Z_{1}\)を\(\Delta Z_{1}\)分微小変化させたとき、中央の電流計に流れる電流\(\Delta I\)を補償定理を用いて求めよ。
補償定理とは
電流\(I_{o}\)が流れている枝にインピーダンス\(\Delta Z\)を接続したときに発生する電流\(\Delta I\)は、回路に接続されている電源を全て殺し、電流の向きと反対に\(\Delta V=\Delta Z I_{o}\)の電圧源を接続したときに流れる電流に等しいことを言います。
長文で申し訳ないですが、上記の操作を手順で表すと下記になります。
- 変化させるインピーダンスに流れる電流\(I_{o}\)を求める。
- インピーダンスの変化幅\(\Delta Z\)を乗算した電圧源\(\Delta ZI_{o}\)を電流と逆向きに接続する。
- 他の電源の影響を全て排除した状態で、変化させたインピーダンスに流れる電流を求める。
結局、操作としては上記3つを行うことで解決できます。微小変化を考えていることから、パラメータは変化前後で一定とみなせます。よって、接続する電圧源は\(\Delta ZI_{o}\)と変化前の電流で考えて良いと考えられます。
補償定理と聞くと、難しいことをやっていそうに見えます。しかし、結論は、電流の変化量を求めるのだから、変化前後のパラメータを調べるという基本的な操作を電気回路として表現しただけです。
実際に例題を解いてみましょう。
解答例
まず、インピーダンス\(Z_{1}\)の変化前の値は、ブリッジ回路の平衡条件により
\begin{aligned}Z_{1}Z_{4}=Z_{2}Z_{3}\end{aligned}
\begin{aligned}Z_{1}=\dfrac{Z_{2}Z_{3}}{Z_{4}}\end{aligned}
この時に流れる電流\(I_{o}\)は
\begin{aligned}I_{o}&=\dfrac{E}{Z_{1}+Z_{3}}\\ &=\dfrac{Z_{4}E}{(Z_{2}+Z_{4})Z_{3}}\end{aligned}
\(Z_{1}\)に対し、\(\Delta Z_{1}\)変化させたときに発生する電流は、検流計に流れる電流と等しい。
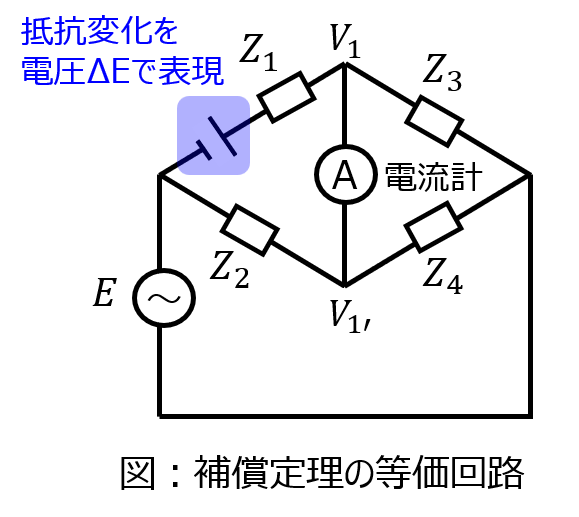
補償定理より、電流と逆向きに接続する電圧源\(\Delta E\)は
\begin{aligned}\Delta E &= \Delta Z_{1}I_{o} \\ &=\dfrac{\Delta Z_{1} Z_{4}E}{(Z_{2}+Z_{4})Z_{3}}\end{aligned}
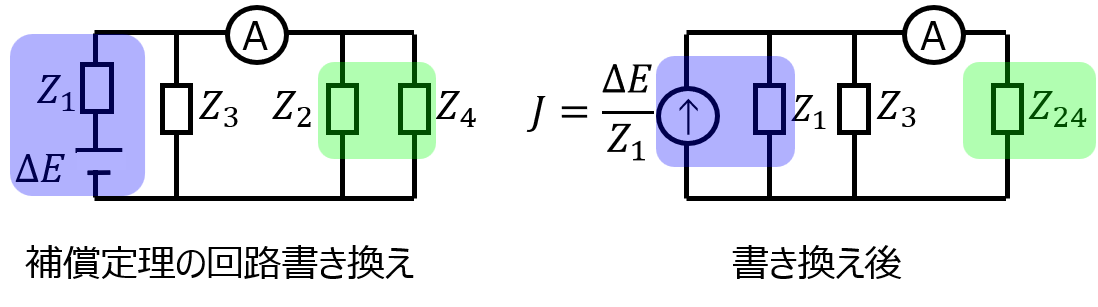
\(\Delta E\)に関係ない電圧源を殺したとき、回路は電流計を中心として下記のように書き直せる。
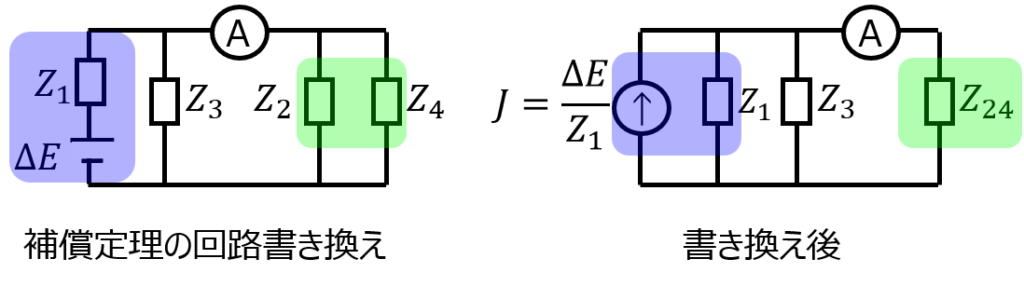
回路の左側を電流源\(\Delta J\)、右側を合成抵抗\(Z_{24}\)に変換すると
\begin{aligned}\Delta J &=\dfrac{\Delta E}{Z_{1}} \\ &=\dfrac{\Delta Z_{1}Z_{4}E}{Z_{1}Z_{3}(Z_{2}+Z_{4})}\end{aligned}
\begin{aligned}Z_{24}=\dfrac{Z_{2}Z_{4}}{Z_{2}+Z_{4}}\end{aligned}
以上より、回路に流れる電流\(\Delta I\)は、分圧則により
\begin{aligned}\Delta I &=\dfrac{\dfrac{1}{Z_{24}}}{\dfrac{1}{Z_{1}}+\dfrac{1}{Z_{3}}+\dfrac{1}{Z_{24}}}\Delta J \\ &=\dfrac{Z_{1}Z_{3}}{Z_{3}Z_{24}+Z_{1}Z_{24}+Z_{1}Z_{3}}\dfrac{\Delta Z_{1}Z_{4}E}{Z_{1}Z_{3}(Z_{2}+Z_{4})}\end{aligned}