【過渡現象】初期値の定理、最終値の定理と電流の極限

電気回路

2025.05.29

問題

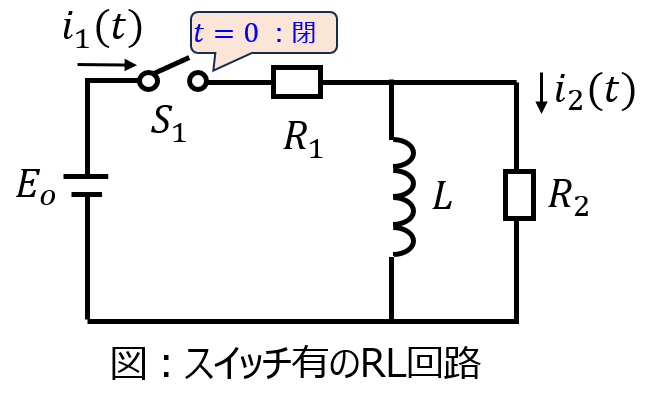
下記の電気回路の抵抗 $R_{2}$ に流れる電流 $i_{2} (t)$ を求めよ。また、t=0,∞の極限における電流 $i (0), i (\infty)$ を求め、初期値の定理、最終値の定理と一致することを確かめよ。

初期値(最終値)の定理とは
1. どのような時に役立つのか？
解答例
1. 補足
最後に

初期値(最終値)の定理とは

ラプラス変換(s領域)のまま、時間領域(t=0)の値、(t=∞)の極限を求めることができる方法です。

時間領域の関数を $f (t)$ 、ラプラス変換後の関数を $F (s)$ とすると、下記の式でそれぞれ表されます。

$\begin{matrix} (1) & {\begin{cases} f (0) = lim_{s \to + \infty} s F (s) \\ f (+ \infty) = lim_{s \to 0} s F (s) \end{cases} \end{matrix}$

ラプラス変換した関数にsを乗算し、時間領域と逆向きの極限を考えることで、求めたい原関数の値を求められることを意味しています。

どのような時に役立つのか？

過渡現象の回路計算を行っている時の検算に使えます。

十分時間が経ったとき、時間領域では、コイルは短絡、コンデンサは開放することで回路に流れる電流、電圧の極限を求めることができます。

ただ単に、極限だけを要求されているだけならばこれで十分かもしれません。しかし、院試だとある時間tにおける電流の時間関数も求めさせられます。よって、ラプラス変換の使用は避けては通れません。

ここで付き物なのが計算ミスです。複雑な回路方程式ほどリスクが高くなります。

このとき、最終値の定理、初期値の定理が役立ちます。今s領域で計算しているパラメータの極限が回路のイメージと合っているのかを逐次確かめることができます。途中の検算的な要素で役立ちます。

解答例

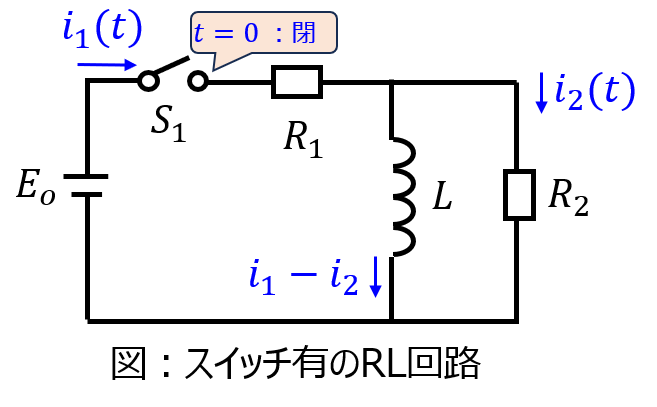
回路方程式は下記で表される。

$\begin{matrix} (2) & {\begin{cases} E_{o} = R_{1} i_{1} (t) + R_{2} i_{2} (t) \\ R_{2} i_{2} (t) = L \frac{d}{d t} (i_{1} (t) - i_{2} (t)) \end{cases} \end{matrix}$

これをラプラス変換すると

$\begin{matrix} (3) & {\begin{cases} \frac{E_{o}}{s} = R_{1} I_{1} (s) + R_{2} I_{2} (s) \\ R_{2} I_{2} (s) = L s (I_{1} (s) - I_{2} (s)) \end{cases} \end{matrix}$

これを $I_{2} (s)$ について解く。上記の第二式より

$\begin{matrix} (4) & \begin{array}{r} I_{1} (s) = \frac{L s + R_{2}}{L s} I_{2} (s) \end{array} \end{matrix}$

これを第一式に代入すると

$\begin{matrix} (5) & \begin{aligned} \frac{E_{o}}{s} & = R_{1} \frac{L s + R_{2}}{L s} I_{2} (s) + R_{2} I_{2} (s) \\ I_{2} (s) & = \frac{L E_{o}}{L (R_{1} + R_{2}) s + R_{1} R_{2}} \end{aligned} \end{matrix}$

上式を用いて、電流 $i_{2} (t)$ におけるt=0,t→∞の極限を初期値、最終値の定理を使用して求める。

まず、t=0のとき

$\begin{matrix} (6) & \begin{aligned} f (0) & = lim_{s \to \infty} s \frac{L E_{o}}{L (R_{1} + R_{2}) s + R_{1} R_{2}} \\ = lim_{s \to \infty} \frac{L E_{o}}{L (R_{1} + R_{2}) + \frac{R_{1} R_{2}}{s}} \\ = \frac{E_{o}}{R_{1} + R_{2}} \end{aligned} \end{matrix}$

回路が初期状態のとき、コイルは開放して考える。このため、抵抗 $R_{1}, R_{2}$ の直列回路になることから上記の計算結果は一致する。

次にt→∞のときを考える。

$\begin{matrix} (7) & \begin{aligned} f (\infty) & = lim_{s \to 0} s \frac{L E_{o}}{L (R_{1} + R_{2}) s + R_{1} R_{2}} \\ = 0 \end{aligned} \end{matrix}$

回路が定常状態のとき、コイルは短絡して考える。このため、抵抗 $R_{2}$ には電流 $i_{2}$ が流れないことからも回路上の振る舞いと一致する。

補足

一応、(5)式を最後まで計算し、ラプラス逆変換できる形にします。その後、時間領域の関数まで求め、極限が一致することも確かめます。

$\begin{matrix} (8) & \begin{array}{r} I_{2} (t) = \frac{E_{o}}{R_{1} + R_{2}} \frac{1}{s + \frac{R_{1} R_{2}}{R_{1} + R_{2}}} \end{array} \end{matrix}$