【過渡現象】電荷保存則を用いたコンデンサに溜まる電荷の計算問題

問題

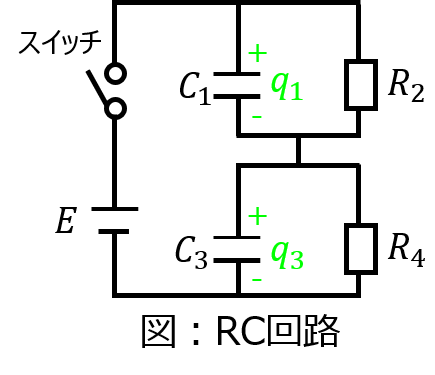
下記のRC回路を考える。t<0ではスイッチが開放されている状態で、t=0のときにスイッチを閉じた。このとき、コンデンサ $C_{1}, C_{3}$ に蓄えられる電荷 $q_{1}, q_{3}$ の時間変化を求めよ。ただし、各コンデンサに蓄えられている初期電荷は0とする。

はじめに
解答例
最後に
参考文献

はじめに

皆様は本問を見て、どのような解答方針を考えたでしょうか。

t<0では、コンデンサに電荷が貯まっていないので、t=0のとき、コンデンサに溜まる電荷は0である初期条件を与えて、回路方程式を解くと考えた方が居るかもしれません。

しかし、実際にこの解き方をすると、ある一つの矛盾が発生することが後々分かります。正しい答えが導けないです。電荷保存則に基づいて初期条件を与えると、解決する様を見ていきましょう。

解答例

全体方針

過渡現象は、微分方程式で示された回路方程式を数学的に解いていく作業です。

回路素子は全て線形であるため、線形微分方程式となります。これの解き方として、下記の常套手段が有ります。

線形微分方程式の解き方

回路方程式を変数項と定数項と左辺右辺に分けて下記1.2.の結果を足し合わせる。
3.で特殊解を決定する。

過渡項：定数項を0にし、変数 $x = A e^{- a t}$ なる一般解を仮定し、回路方程式に代入。過渡解を求める。
定常項：t→∞になったときの回路の状態によって、目的の変数の最終的な値を決定。
t=0のときの初期条件を与え、未知数Aを求める。(特殊解)

過渡現象の計算は、このような作業で解くことができます。文字だけで説明しても難しいので、実際に下記で計算していきましょう。

回路方程式の立式

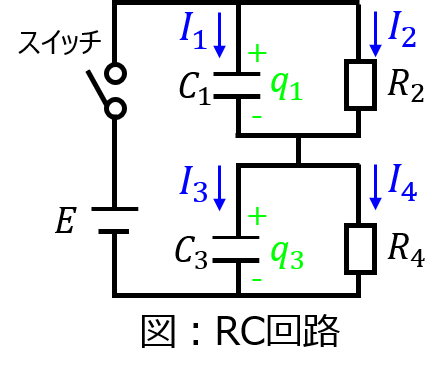
コンデンサ $C_{1}, C_{3}$ 、抵抗 $R_{2}, R_{4}$ の添え字に対応する電流変数 $I_{1}, I_{2}, I_{3}, I_{4}$ を設定すると、電流則は

$\begin{matrix} (1) & \begin{array}{r} I_{1} + I_{2} = I_{3} + I_{4} \end{array} \end{matrix}$

$I = \frac{d q}{d t} = \frac{V}{R} = \frac{Q}{R C}$ の関係を利用すると

$\begin{matrix} (2) & \begin{array}{r} \frac{d q_{1}}{d t} + \frac{q_{1}}{R_{2} C_{1}} = \frac{d q_{3}}{d t} + \frac{q_{3}}{R_{2} C_{1}} \end{array} \end{matrix}$

電圧則についても立式すると

$\begin{matrix} (3) & \begin{array}{r} E = \frac{d q_{1}}{d t} + \frac{q_{3}}{C_{3}} \\ q_{3} = C_{3} E - \frac{C_{3}}{C_{1}} q_{1} \end{array} \end{matrix}$

式(3)を(2)に代入すると

$\begin{matrix} (4) & \begin{array}{r} \frac{d q_{1}}{d t} + \frac{q_{1}}{R_{2} C_{1}} = - \frac{C_{3}}{C_{1}} \frac{d q_{1}}{d t} + \frac{1}{R_{4} C_{3}} (C_{3} E - \frac{C_{3}}{C_{1}} q_{1}) \end{array} \end{matrix}$

$\begin{matrix} (5) & \begin{array}{r} \frac{E}{R_{4}} = (1 + \frac{C_{3}}{C_{1}}) \frac{d q_{1}}{d t} + (\frac{1}{R_{2} C_{1}} + \frac{1}{R_{4} C_{1}}) q_{1} \end{array} \end{matrix}$

過渡項の計算

上記は線形微分方程式のため、過渡解 $q_{1 t}$ を下記のように置く。

$\begin{matrix} (6) & \begin{array}{r} q_{1 t} = A e^{- a t} \end{array} \end{matrix}$

(5)式の左辺(定数項)を0と置くと、特性方程式

$\begin{matrix} (7) & \begin{array}{r} 0 = - a (1 + \frac{C_{3}}{C_{1}}) A e^{- a t} + (\frac{1}{R_{2} C_{1}} + \frac{1}{R_{4} C_{1}}) A e^{- a t} \end{array} \end{matrix}$

$\begin{matrix} (8) & \begin{aligned} a & = \frac{(\frac{1}{R_{2} C_{1}} + \frac{1}{R_{4} C_{1}})}{(1 + \frac{C_{3}}{C_{1}})} \\ = \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} \end{aligned} \end{matrix}$

定常項の計算、過渡項との足し合わせ

定常項を $q_{1 s}$ とする。定常状態のとき、コンデンサに電流は流れず、抵抗 $R_{2}, R_{4}$ の分圧で $C_{1}$ にかかる電圧 $V_{1}$ が決まる。

$\begin{matrix} (9) & \begin{array}{r} V_{1} = \frac{q_{1 s}}{C_{1}} = \frac{R_{2}}{R_{2} + R_{4}} E \end{array} \end{matrix}$

$\begin{matrix} (10) & \begin{array}{r} q_{1 s} = \frac{R_{2} C_{1}}{R_{2} + R_{4}} E \end{array} \end{matrix}$

以上より、コンデンサ $C_{1}$ に溜まる電荷の時間変化は

$\begin{matrix} (11) & \begin{aligned} q_{1} & = q_{1 s} + q_{1 t} \\ = \frac{R_{2} C_{1}}{R_{2} + R_{4}} E + A e^{- \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} t} \end{aligned} \end{matrix}$

最後に、手順3.で特殊解を求めます。t=0のときの電荷の初期条件を与え、未知数 $A$ を求める。これの与え方に注意が必要です。

手順3.よくある誤答

t=0のとき、初期電荷 $q_{1} = 0$ を(11)式に代入し

$\begin{matrix} (12) & \begin{array}{r} A = \frac{R_{2} C_{1}}{R_{2} + R_{4}} E \end{array} \end{matrix}$

以上より、求める電荷 $q_{1}$ の時間変化は

$\begin{matrix} (13) & \begin{array}{r} q_{1} = \frac{R_{2} C_{1}}{R_{2} + R_{4}} E (1 - e^{- \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} t}) \end{array} \end{matrix}$

回路の対称性により、 $q_{3}$ の時間変化は

$\begin{matrix} (14) & \begin{array}{r} q_{1} = \frac{R_{4} C_{3}}{R_{2} + R_{4}} E (1 - e^{- \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} t}) \end{array} \end{matrix}$

以上が求める解である。

・・・どの部分が間違っているか、気づきましたでしょうか。

この解の与え方だと、t=+0のとき、コンデンサ部分に全く電圧がたたず、回路の電圧則を満たさないです。

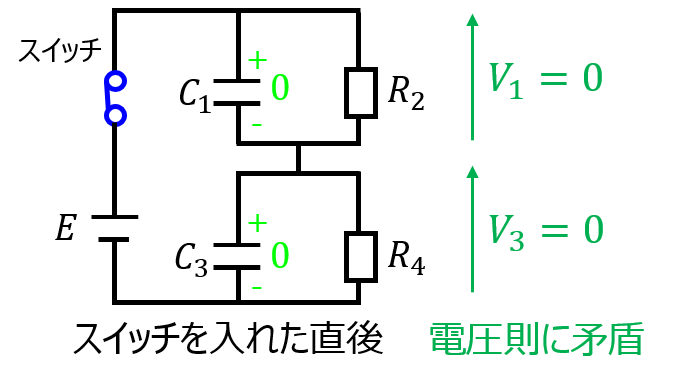
コンデンサ $C_{1}, C_{3}$ で発生する電圧をそれぞれ $V_{1}, V_{3}$ とすると、 $V_{1} + V_{3} = E$ である必要がありますが、上記の場合電荷が0です。 $V_{1} = V_{3} = 0$ となり、矛盾します。

では、どうすれば良いのでしょうか？答えは、電荷の連続性(電荷保存則)に注目すれば良いです。

手順3.正しい解き方

電荷保存則により、スイッチを閉じる前後の電荷の関係は下記のようになる。

$\begin{matrix} (15) & \begin{array}{r} - q_{1} (- 0) + q_{3} (- 0) = - q_{1} (+ 0) + q_{3} (+ 0) \end{array} \end{matrix}$

スイッチを閉じた瞬間、電圧則により下記の関係が成立する。

$\begin{matrix} (16) & \begin{array}{r} \frac{q_{1} (+ 0)}{C_{1}} + \frac{q_{3} (+ 0)}{C_{3}} = E \end{array} \end{matrix}$

$\begin{matrix} (17) & \begin{array}{r} q_{1} (+ 0) = q_{3} (+ 0) = \frac{C_{1} C_{3}}{C_{1} + C_{3}} E \end{array} \end{matrix}$

これを(11)式に代入すると

$\begin{matrix} (18) & \begin{array}{r} A = \frac{(R_{4} C_{3} - R_{2} C_{1}) C_{1}}{(R_{2} + R_{4}) (C_{1} + C_{3})} \end{array} \end{matrix}$

よって、求める $q_{1}$ の時間変化は

$\begin{matrix} (19) & \begin{array}{r} q_{1} = \frac{R_{2} C_{1}}{R_{2} + R_{4}} E + \frac{(R_{4} C_{3} - R_{2} C_{1}) C_{1}}{(R_{2} + R_{4}) (C_{1} + C_{3})} e^{- \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} t} \end{array} \end{matrix}$

回路の対称性により、 $q_{3}$ の時間変化は

$\begin{matrix} (20) & \begin{array}{r} q_{3} = \frac{R_{4} C_{3}}{R_{2} + R_{4}} E + \frac{(R_{2} C_{1} - R_{4} C_{3}) C_{1}}{(R_{2} + R_{4}) (C_{1} + C_{3})} e^{- \frac{R_{2} + R_{4}}{R_{2} R_{4} (C_{1} + C_{3})} t} \end{array} \end{matrix}$