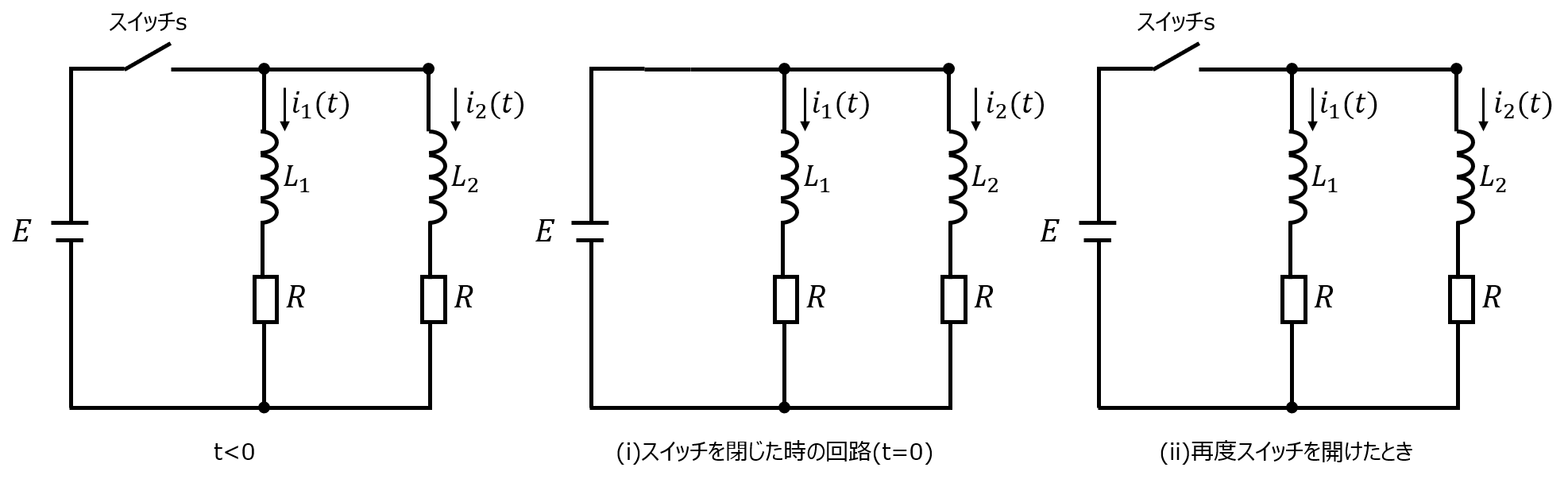【過渡現象】鎖交磁束不変の理を利用した過渡電流の算出

電気回路

2024.05.022025.02.01

問題

下記のLR並列回路を考える。(i) $t = 0$ でスイッチを閉じて、(ii)十分に時間が経過してからスイッチを開く。
(i)(ii)における電流 $i_{1}, i_{2}$ をそれぞれ求めよ。

はじめに
解答例
最後に

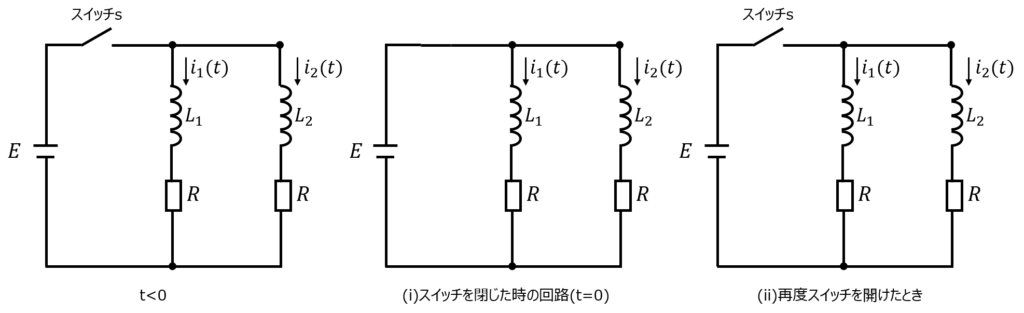
はじめに

本問は一つ気を付ける箇所があります。

$t = 0$ でスイッチを閉じてそのまま十分な時間が経過する設定ならば普通の問題ですが、そのあとスイッチを開きます。ここでの立式を間違えてしまうと、正解することはできません。

解答例

(i)スイッチを閉じた時の電流値

ここは、普通に微分方程式を解いていけば良いです。管理人はラプラス変換を用います。

まず、電流 $i_{1} (t)$ について、回路方程式より

$\begin{array}{r} (1) & E = L_{1} \frac{d i_{1}}{d t} + R i_{1} (t) \end{array}$

これをラプラス変換して

$\begin{array}{r} (2) & \frac{E}{s} = L s I_{1} (s) - L i (0) + R I_{1} (s) (s) \end{array}$

$t = 0$ 以前はスイッチが開かれているので、 $i (0) = 0$

$\begin{matrix} (3) & \begin{aligned} I_{1} (s) & = \frac{E}{s (4 s + R)} \\ = \frac{E}{L_{1}} \frac{1}{s (s + \frac{R}{L_{1}})} \\ i_{1} (t) & = \frac{E}{R} (1 - e^{- \frac{R}{L_{1}} t}) \end{aligned} \end{matrix}$

電流 $i_{2} (t)$ について、回路方程式より

$\begin{array}{r} (4) & E = L_{2} \frac{d i_{2}}{d t} + R i_{2} (t) \end{array}$

$L_{1} \Rightarrow L_{2}$ で置き換えた形なので、同様にして

$\begin{matrix} (5) & \begin{array}{r} i_{1} (t) = \frac{E}{R} (1 - e^{- \frac{R}{L_{1}} t}) \end{array} \end{matrix}$

(ii)再度スイッチを開いた時の電流値

電圧源と切り離されており、 $i_{1} = i_{2}$ なので、回路方程式より

$\begin{array}{r} (6) & R i (t) + L_{1} \frac{d i_{1}}{d t} + R i (t) + L_{2} \frac{d i_{1}}{d t} = 0 \end{array}$

これをラプラス変換して

$\begin{array}{r} (7) & R I (s) + L_{1} s I (s) - L_{1} i_{1} + R I (s) + L_{2} s I (s) - L_{2} i_{2} = 0 \end{array}$

これを整理し、 $i_{1} (t)$ を求める方針に変わりないですが、(7)式の $i_{1}, i_{2}$ に入れる数字が肝です。

誤答例

十分に時間が経った時、 $i_{1} (\infty) = i_{2} (\infty) = \frac{E}{R}$

よって、これを回路方程式(7)の $i_{1}, i_{2}$ に代入して解を得る。

・・・・・・・・・・・・・・・

こちらの間違いに皆様は気づきましたでしょうか。
スイッチを閉じる前の電流値であるため、閉じた後の回路方程式には適用できないです。

では、どうやって閉じた瞬間の電流値を求めるのでしょうか。ここで出てくるのが、鎖交磁束不変の理です。

スイッチを閉じる前後で電流値は変化しても、コイルを貫く磁束の総数は変化しない法則です。

$\begin{array}{r} (8) & L_{1} i_{1 前} + L_{2} i_{2 前} = L_{1} i_{1 後} + L_{2} i_{2 後} \end{array}$

で表すことができます。(前は、スイッチを操作する前の電流値、後は、スイッチを操作した直後の電流値を示しています。)

正しい解答例

鎖交磁束不変の理を考える。 $i_{1 前} = i_{2 前} = \frac{E}{R}$ より

$\begin{array}{r} (9) & \frac{L_{1} E}{R} + \frac{L_{2} E}{R} = (L_{1} + L_{2}) i_{1 後} \\ (10) & i_{1 後} = \frac{L_{1} - L_{2}}{R (L_{1} + L_{2})} E \end{array}$

これを(7)に代入し

$\begin{matrix} (11) & \begin{array}{r} (2 R + (L_{1} + L_{2}) s) I_{1} (s) = \frac{(L_{1}^{2} - L_{2}^{2})}{R (L_{1} + L_{2})} E \\ I (s) = \frac{(L_{1} - L_{2})}{R (L_{1} + L_{2})} \frac{E}{s + \frac{2 R}{L_{1} + L_{2}}} \end{array} \end{matrix}$