下記の導体間の相互インダクタンス\(M\)を求めよ。
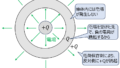
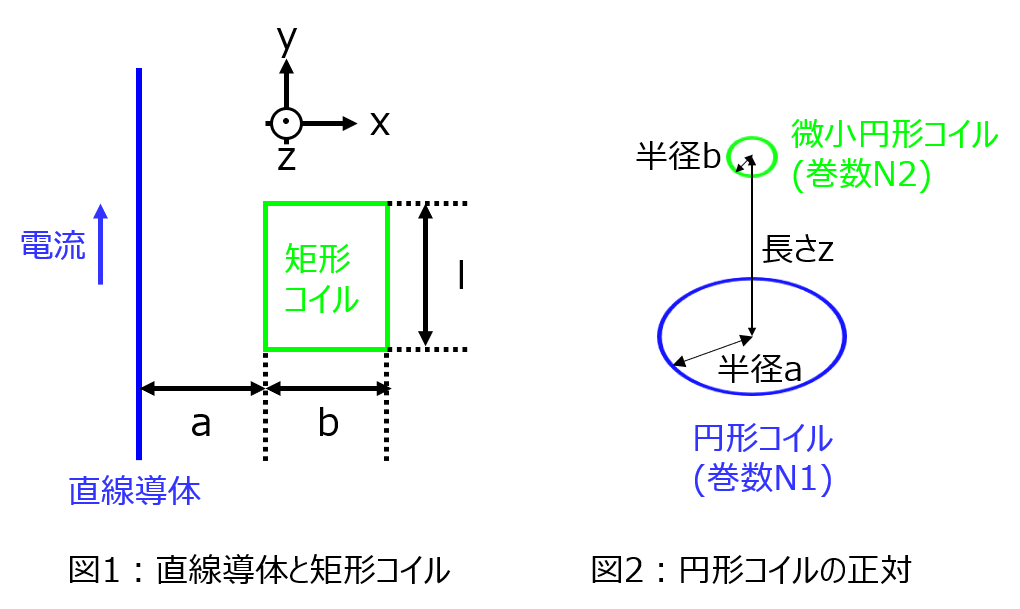
(1)無限遠に延びる直線導体と\(r=a\)離れた位置に存在する\(x\)方向に\(b\)、\(y\)方向に\(l\)離れた矩形コイル。
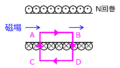
(2)半径\(a\)巻き数\(N_{1}\)の円形コイルと、半径\(b\)、巻き数\(N_{2}\)の微小円形コイルが距離z離れて正対している。両者のコイル間の相互インダクタンスを求めよ。なお、半径\(b\)のコイルは非常に小さく、内部を貫く磁場は一定とする。
相互インダクタンスとは
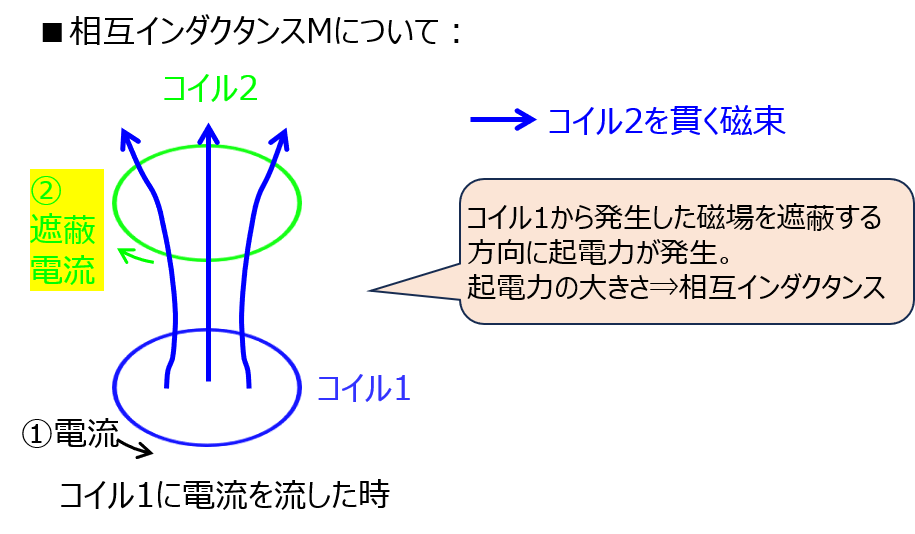
あるコイル1に電流を流した時に発生した磁場が別のコイル2を貫いた時、発生する誘導起電力の関係を示した係数です。
下記の式で表されます。
\begin{cases}\Phi_{2}=M_{12}I_{1} \\ |V|=\dfrac{d \Phi_{2}}{dt}=M_{12}\dfrac{dI_{1}}{dt}\end{cases}
また、コイル2に電流を流した時にコイル1で発生する誘導起電力の関係は\(M_{21}\)で表されます。
\begin{cases}\Phi_{1}=M_{21}I_{2} \\ |V|=\dfrac{d \Phi_{1}}{dt}=M_{21}\dfrac{dI_{2}}{dt}\end{cases}
対称性から、\(M_{12}=M_{21}\)の関係があります。
なお、コイル1に電流を流した時に発生する磁場がコイル1を貫いて発生する起電力を表す係数は自己インダクタンスと言います。
\begin{cases}\Phi_{1}=L_{11}I_{1} \\ |V|=\dfrac{d \Phi_{1}}{dt}=L_{11}\dfrac{dI_{1}}{dt}\end{cases}
コイル2に関しても同様で、\(L_{22}\)で表される。
結合係数
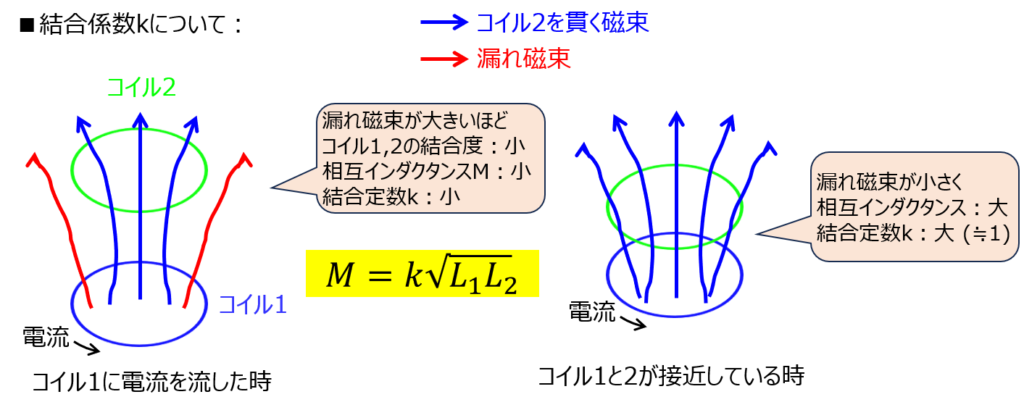
コイル1に電流を流し発生した磁場は全てコイル2を貫くわけではありません。貫かない磁場を漏れ磁束と言い、その分だけコイル2の誘導起電力に寄与しなくなります。
よって、コイル1-2の間の相互インダクタンス\(M_{12}=M_{21}\)は、それぞれのコイルの自己インダクタンス\(L_{11},L_{22}\)以下になるため、下記の式で表されます。
\begin{aligned}M_{12}≦\sqrt{L_{11}L_{21}}\end{aligned}
上式に等号=を成立するために結合定数\(k\) \(0≦k≦1\)を設定し
\begin{aligned}M_{12}=k\sqrt{L_{11}L_{21}}\end{aligned}
の表され方をする場合があります。\(k\)が1に近いほど、漏れ磁束が少なく、自己インダクタンスと相互インダクタンスの差が少ないです。
解答例
方針
前章のように、コイル1に電流\(I_{1}\)を流した時にコイル2に流れる鎖交磁束\(\Phi_{2}\)を計算すれば良いです。
- 無限遠に延びる直線導体と矩形コイルの場合:アンペールの法則で直線導体から発生する磁束密度を計算し、矩形コイルの存在範囲を積分する。
- 円形コイルの場合:ビオサバールの法則で中心軸における磁束密度を計算する。
以上の観点で解いていけば良いです。アンペールの法則、ビオサバールの法則の適用条件は、こちらの記事で詳しく説明しています。
(1)直線導体と矩形コイルの相互インダクタンス
アンペールの法則より、直線導体に電流\(I_{1}\)を流したとき、半径\(r\)離れた磁束密度\(B\)は
\begin{aligned}B=\dfrac{\mu_{o}I_{1}}{2 \pi r}\end{aligned}
矩形コイルを貫く磁束\(\Phi_{2}\)を考える。上式Bをr:[a,a+b]の間で積分し、y方向の長さが\(l\)なので、結果を\(l\)倍すれば良い。
\begin{aligned}\Phi_{2}&=l*\int^{a+b}_{a}\dfrac{\mu_{o}I_{1}}{2 \pi r} dr \\ &= \dfrac{\mu_{o} l I_{1}}{2 \pi}\log\dfrac{a+b}{a}\end{aligned}
\(\Phi_{2}=M_{12}I_{1}\)より、求める相互インダクタンス\(M_{12}\)は
\begin{aligned}M_{12}=\dfrac{\mu_{o} l }{2 \pi}\log\dfrac{a+b}{a}\end{aligned}
(2)微小円形コイルとの相互インダクタンス
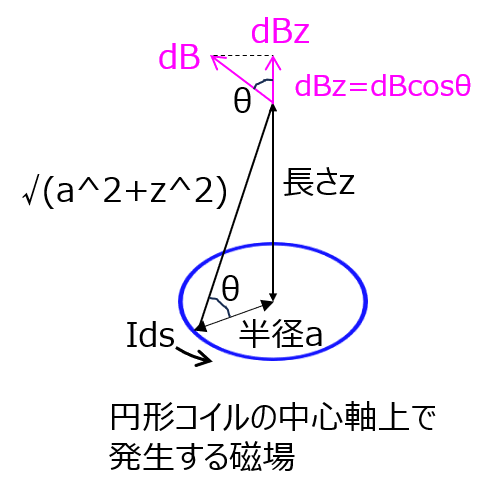
ビオサバールの法則より、コイル1からz離れたコイル2における磁束密度\(B\)を求める。\(r=\sqrt{a^{2}+z^{2}}\)とすると、円環の微小電流要素\(Ids\)による磁場は下記のようになる。
\begin{aligned}dB=\dfrac{\mu_{o}I_{1}ds}{4 \pi r^{2}}\end{aligned}で、コイル1を周回積分したとき、z成分以外は打ち消し合うので
\begin{aligned}dB_{z}=dB\dfrac{a}{r}\end{aligned}
を円周\(2 \pi a\)で周回積分する。巻き数が\(N_{1}\)であることを考慮して
\begin{aligned}B_{z}&=\dfrac{\mu_{o}IaN_{1}}{4 \pi r^{3}}\int_{c}ds \\ &=\dfrac{\mu_{o}I_{1}aN_{1}}{4 \pi r^{3}}(2 \pi a) \\ &= \dfrac{\mu_{o}I_{1}a^{2}N_{1}}{2 (a^{2}+z^{2})^{3/2}}\end{aligned}
微小円形コイルの磁束の鎖交面積は\(S_{2}= \pi b^{2}\)。この分を上式Bが巻き数\(N_{2}\)回分鎖交するので、求める磁束は
\begin{aligned}\Phi_{2}&=N_{2}B_{z}S_{2} \\ &=\dfrac{\pi \mu_{o}I_{1}a^{2}b^{2}N_{1}N_{2}}{2 (a^{2}+z^{2})^{3/2}}\end{aligned}
以上より、求める相互インダクタンス\(\Phi_{2}=M_{12}I_{1}\)は
\begin{aligned}M_{12}=\dfrac{\pi \mu_{o}a^{2}b^{2}N_{1}N_{2}}{2 (a^{2}+z^{2})^{3/2}}\end{aligned}
補足
(2)は、コイル2の面積が微小だったため、鎖交磁束\(\Phi_{2}\)(11)式の計算が楽にできました。ですが、コイル2も大型になり、尚且つコイル1と近づいた位置に配置した際はこの仮定が使えなくなります。