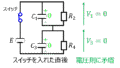
下記の電気回路(a)(b)において、抵抗R、コンデンサCに流れる電流の時間変化を求めよ。
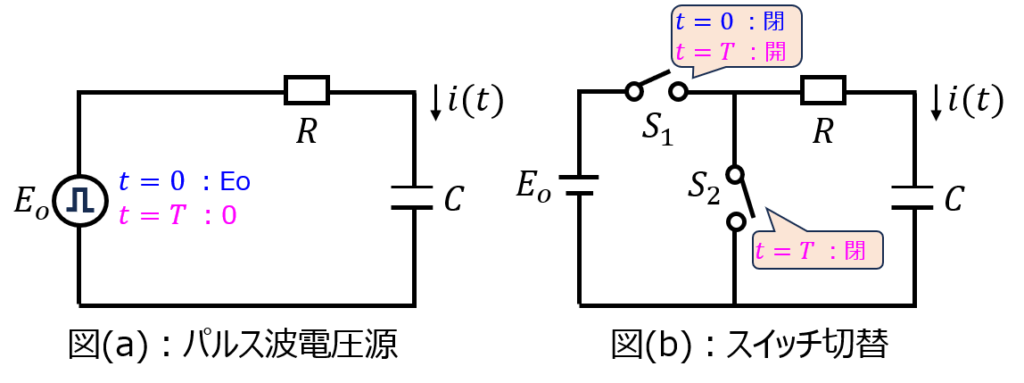
(a)t=0で電圧\(E_{o}\)が立ち上がり、t=Tで電圧が0に立ち下がる電圧源
(b)直流電流源\(E_{o}\)に対し、t=0でスイッチ\(S_{1}\)を閉め、t=Tでスイッチ\(S_{1}\)を開くと同時に\(S_{2}\)を閉める電気回路
はじめに
本問は、過渡現象の問題の中で一捻りきいたものになります。電圧\(E_{o}\)が十分時間が経つまで接続しているのではなく、一定時間経過した後に0に立ち下がるorスイッチで遮断するものになっています。
この動作を回路方程式として表現できるかが鍵になります。下記に考え方を示していきます。
パルス波のラプラス変換
まず、上記の計算が出来るかが肝になります。ラプラス変換の公式
\begin{aligned}F(s)=\int^{\infty}_{0}f(t)e^{-st}dt\end{aligned}
を用いると、問題(a)で与えられている電圧は、t=0~Tの間だけ\(E_{o}\)。それ以外は0を取ることから
\begin{aligned}E(s)&=\int^{T}_{0} E_{o}e^{-st}dt \\ &=\dfrac{E_{o}}{s}\left(1-e^{-sT}\right)\end{aligned}
になります。\(e^{-sT}\)は時間遅れ要素です。ステップ関数u(t)を用いてラプラス逆変換すると\(u(t-T)\)になります。
t=Tのとき、ステップ成分1が立つ。と言うわけですね。
(逆に、\(\frac{E_{o}}{s}\)を逆変換すると\(E_{o}u(t)\)となります。t=0でステップ成分が立ちます。)
回路方程式上のパルス波の表現方法
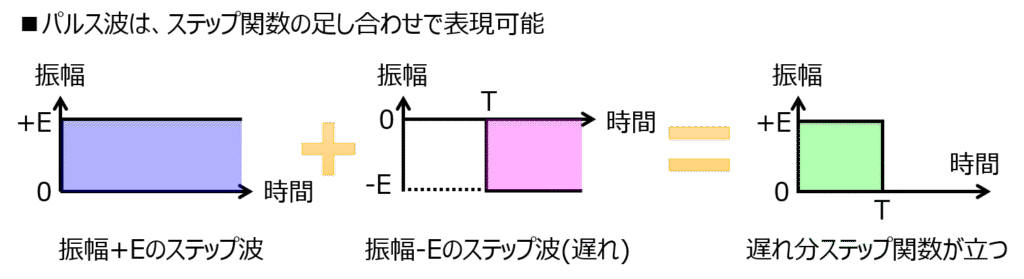
-u(t-T)について、今回の式では符号が負になっています。よって、t=0~Tの間はu(t)のみが成立し、1が立つが、t=T以降は負のステップ成分-u(t-T)も立ち、両者が相殺することで0を表現できる。という解釈ができます。
このように、パルス波(矩形波)は、ステップ関数の重ね合わせで表現できます。
解答に際して
パルス波の計算方法さえ分かれば、後は回路方程式に基づいて目的の変数(今回は電流\(i(t)\))を求めることに帰着します。
\(e^{-at}\)が付くと、時間遅れ要素になる。これが本記事の合言葉です。
解答例
(a)パルス波の電圧源

前節で説明したラプラス変換方法を用いて解いていきます。
時間領域の回路方程式は
\begin{aligned}E_{o}u(t)-E_{o}u(t-T)=Ri(t)+\dfrac{1}{C}\int^{t}_{0}i(t)e^{-st}dt\end{aligned}
これをラプラス変換して
\begin{aligned}\dfrac{E_{o}}{s}\left(1-e^{-sT}\right)=RI(s)+\dfrac{I(s)}{Cs}\end{aligned}
\(I(s)\)について解くと
\begin{aligned}I(s)&=\dfrac{E_{o}}{s}\dfrac{Cs}{RCs+1}\left(1-e^{-sT}\right) \\ &=\dfrac{E_{o}}{R}\dfrac{1}{s+\frac{1}{RC}}\left(1-e^{-sT}\right)\end{aligned}
これをラプラス逆変換して
\begin{aligned}i(t)=\dfrac{E_{o}}{R}e^{\frac{t}{RC}}-\dfrac{E_{o}}{R}e^{\frac{t-T}{RC}}u(t-T)\end{aligned}
第1項はt=0で電圧が立ち上がるステップ成分、第2項がt=Tで電圧が立ち下がる成分を指しています。
(b)スイッチの切り替えによるパルス波
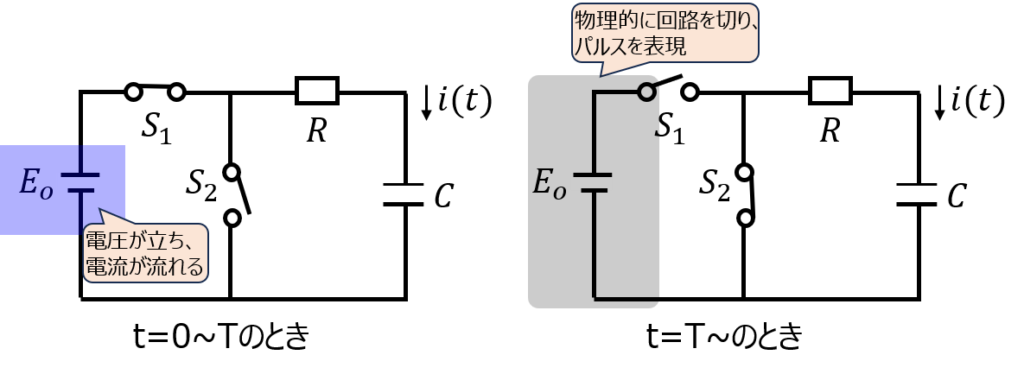
本問を考えていると、気づいたことはありませんか?
t=0で直流電圧源\(E_{o}\)が繋がるが、t=Tで開放します。(分流のため、スイッチ\(S_{2}\)は接続する。)
これは、パルス波の振る舞いそのものになります。よって、(a)と同じ回路方程式になります。
\begin{aligned}E_{o}u(t)-E_{o}u(t-T)=Ri(t)+\dfrac{1}{C}\int^{t}_{0}i(t)e^{-st}dt\end{aligned}
わざわざパルス波電圧源を接続しなくても、スイッチの切り替えで疑似的にパルス波を表現できます。
回路方程式が(a)と同じなので、(b)も答えも(6)式になります。
最後に
電圧源を接続している時にスイッチを切り替える問題は様々な大学の院試で頻出です。本記事には基本的事項がつまっています。