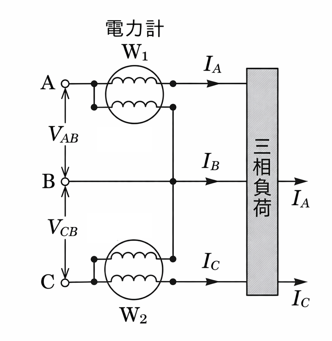
下記に示すように、相電圧$V$の三相交流に、$R=5\sqrt{3}$の抵抗と$X=5$のリアクタンスが接続されている。負荷電流の大きさを$I$、力率角を$\theta$とし、下記の問に答えよ。
問1:電力計$W_1,W_2$の指示値を$I,\theta$を用いて表せ。
問2:各相に流れる負荷電流の大きさ$I$を求めよ。また、力率角$\theta$も求めよ。
問3:$W_1,W_2$の値を求めよ。
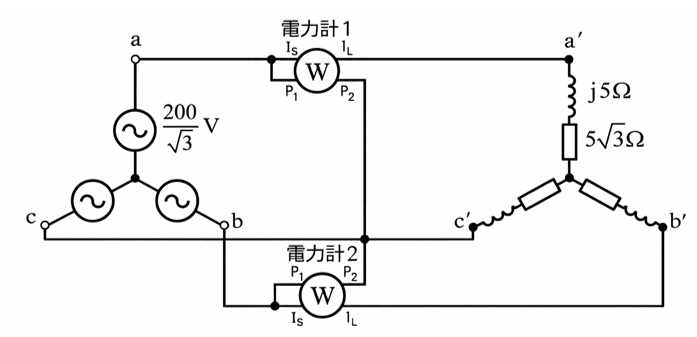
二電力計法とは
三相交流の系統電力は、3-1=2台の電力系の読み値の和で求められることを言います。下記のように、線間電圧が$V$、電線流が$I$の三相交流系統を考え、B相を線間電圧の基準、A相、C相に電力計を置きます。両者の読み値を$P_{1},P_{2}$とすると、三相電力$P$は以下のように表すことが出来ます。
\begin{cases}P=P_{1}+P_{2} \\ P_{1}=VI\cos\left(\dfrac{\pi}{6}+\theta\right) \\ P_{2}=VI\cos\left(\dfrac{\pi}{6}-\theta\right)\end{cases}
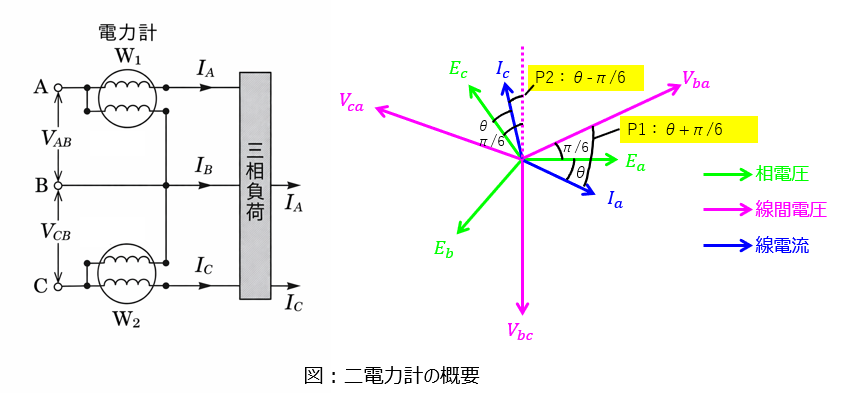
$P_{1},P_{2}$の位相がそれぞれπ/6=30°進んでいる/遅れていることは、線間電圧と相電圧の関係により分かります。
過去の記事で説明したベクトル合成により、線間電圧$V_{ba}$は、基準相電圧$E_{a}$に対してπ/6進むとお話ししました。$E_{b}$に対してはπ/6遅れます。この関係を$P_{1},P_{2}$式に落とし込むことで、π/6のずれを表現できるということですね。なお、$\theta$は、負荷力率を表します。
加法定理を用いることで、三相電力$P$はおなじみの形$P=\sqrt{3}VI\cos \theta$で表すことができます。
\begin{aligned}P&=P_{1}+P_{2} \\ &=VI\left \lbrace \cos\left(\dfrac{\pi}{6}+ \theta\right)+\cos\left(\dfrac{\pi}{6}- \theta\right) \right \rbrace \\ &=VI\left \lbrace \cos\dfrac{\pi}{6}\cos \theta+\sin\dfrac{\pi}{6}\sin\theta+\cos\dfrac{\pi}{6}\cos \theta-\sin\dfrac{\pi}{6}\sin\theta)\right \rbrace \\ &=\sqrt{3}VI\cos\theta\end{aligned}
この考え方は、大阪公立大学の院試にてよく出てきます。同大学を志願する方は、必ず覚えておきましょう。
また、簡単化のために平衡負荷を前提でお話ししましたが、不平衡負荷でも本考え方は成立します。
三相無効電力について
二電力計法は、有効電力だけでなく無効電力$Q$も電流計の指示値の差の√3倍で求められます。
\begin{aligned}Q=\sqrt{3}(P_{1}-P_{2})=\sqrt{3}VI \sin \theta\end{aligned}
導出に関しては、(2)式の考え方をそのまま利用できます。中括弧{}内に存在する二つの項の和+だった部分が差-になり、加法定理をするとsin項が残るためです。
上記の結果を用いて、三角関数$\tan \theta$も下記のように表されます。
\begin{aligned}\tan \theta&=\dfrac{\sqrt{3}VI \sin \theta}{\sqrt{3}VI \cos \theta} \\ &=\dfrac{\sqrt{3}(P_{1}-P_{2})}{P_{1}+P_{2}}\end{aligned}
補足:ブロンデルの定理について
現実世界での電力送電方法は専ら三相交流方式で行われています。よって、試験問題としても二電力計で問われることが殆どですが、一般的に、任意のn線式回路の電力は、(n-1)個の電流計の読み値の和で表すことができます。
これをブロンデルの定理と言います。予備知識として持っておくと、派生問題が出た時に反応しやすくなります。
解答例
誘導に則って求めていけば、自ずと解決できる問題になります。
問1:電力計の読み値
線間電圧が200Vのため、(1)式の考え方を用いる。電力計の線間電圧を計測する基準がc相であることに注意すると、下記のようなベクトル図になる。
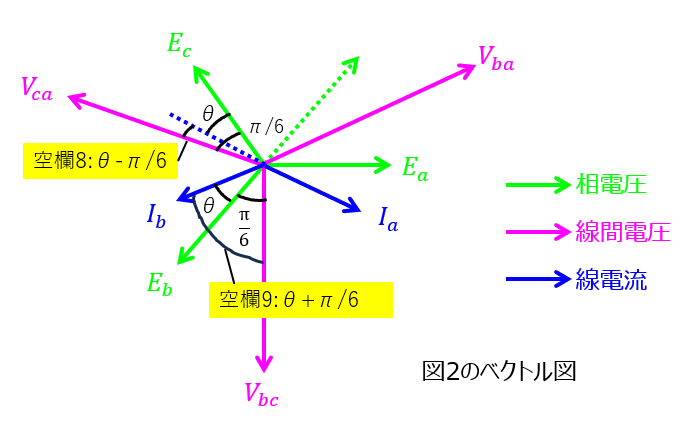
この関係に注意すると
\begin{cases} W_{1}=200I\cos\left(\dfrac{\pi}{6}-\theta\right) \\ W_{2}=200I\cos\left(\dfrac{\pi}{6}+\theta\right)\end{cases}
一言
空欄(8)と(9)は逆にすると、問4の$W_1,W_2$の結果が逆になります。合計値を問われているのであれば気になりませんが、それぞれの値を求める場合は失点に繋がります。(1)式を丸暗記せず、ベクトル図を用いて導出できるようになりましょう。
問2:負荷電流と力率の関係
まず、インピーダンス$Z$を求める。抵抗$R=5\sqrt{3}$、リアクタンス$X=5$により
\begin{aligned}Z&=\sqrt{(5\sqrt{3})^{2}+5^{2}} \\ &=10 [\mathrm{Ohm}]\end{aligned}
相電圧は線間電圧の1/√3倍なので、オームの法則により求める負荷電流は
\begin{aligned}I&=\dfrac{200/\sqrt{3}}{10} \\ &=\dfrac{20}{\sqrt{3}}[\mathrm{A}]\end{aligned}
力率について:$\cos\theta=\frac{R}{Z}=\frac{\sqrt{3}}{2}$なので、$\theta=\frac{\pi}{6}$
問3:各電力計の指示値
問2の結果により
\begin{cases}W_{1}=200I\cos0 \\ W_{2}=200I\cos\dfrac{\pi}{3} \end{cases}
\begin{aligned}W_{1} &=200*\dfrac{20}{\sqrt{3}}[\mathrm{W}] \\ &=\dfrac{4}{\sqrt{3}}[\mathrm{kW}]\end{aligned}
\begin{aligned}W_{2}=\dfrac{2}{\sqrt{3}}[\mathrm{kW}]\end{aligned}
最後に
本問は経験がモノを言います。本記事の問題でも何でも良いので類題を1題は演習しましょう。