【電気回路】相加相乗平均を用いた最大消費電力の算出

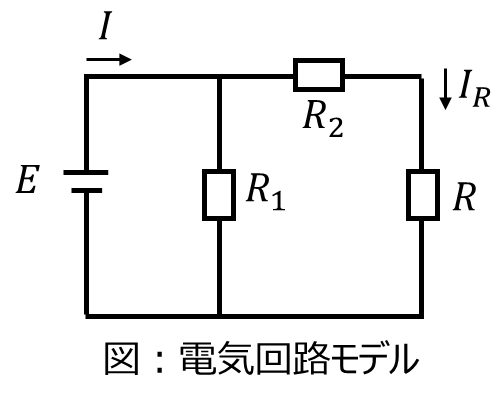
電気回路における消費電力

抵抗Rに電流Iが流れている時、下記の式で表されます。

\begin{aligned}P=RI^{2}\end{aligned}

本問の電気回路を見ると、抵抗\(R_{1}\)から右では\(R_{2}\)と\(R\)に分かれています。

よって、電圧源から流れる電流は、この2つの枝に分岐します。解答に際しては、抵抗\(R\)に流れる電流値を求めてから、変数\(R\)を含む消費電力の式を立てる必要があります。

最大消費電力の計算方法

以下2つの方法があります。

方法1.は任意の電気回路に対して適用できます。高校数学の数Ⅲの微分と行っていることは変わりません。微分の公式さえ覚えていれば解くことができます。

反面、計算量が多くなりがちなデメリットもあります。計算ミスしなければ良いですが、限りある試験時間では厳しいです。

一方で、式によっては方法2.を使えることが有ります。相加相乗平均については、下記の関係になります。

この関係を利用します。変数Rを含む項をa,bの2項に分けられるときに使用できます。等号成立時、最小値になる表記ですが、逆数(分母側)だったとすると最大値になります。

上記の考え方を利用し、少ない計算コストで最大消費電力を求めていきます。

解答例

方法1.で解く方法と方法2.で解く方法を比べてみます。

まず、両者の方法で共通して行うことは、抵抗Rで発生する消費電力の式を立てることです。各論に移る前に、これを先にやります。

抵抗に流れる電流\(I_{R}\)は

\begin{aligned}I_{R}&=\dfrac{E}{R_{1}+\dfrac{RR_{2}}{R+R_{2}}}\dfrac{R_{2}}{R_{2}+R} \\ &=\dfrac{R_{2}E}{R_{1}(R_{2}+R)+RR_{2}}\end{aligned}

よって、求める消費電力\(P\)は

\begin{aligned}P&=RI_{R}^{2} \\ &=\dfrac{R(R_{2}E)^{2}}{\lbrace R_{1}(R_{2}+R)+RR_{2}\rbrace^{2}}\end{aligned}

方法1.微分を使用する場合

こちらは正攻法です。方法2.が本記事で主張したいことですが、対比のために記載します。

(4)式を\(R\)で微分し

\begin{aligned}\dfrac{d P}{d R}&=\dfrac{\lbrace R_{1}(R_{2}+R)+RR_{2}\rbrace^{2}-2R{R_{1}(R_{2}+R)+RR_{2}}(R_{1}+R_{2})}{\lbrace R_{1}(R_{2}+R)+RR_{2}\rbrace ^{4}}R_{2}E^{2}\end{aligned}

Rが0のとき、上式は正となり、Rを増加させると消費電力Pも増加する。分子が0になるとき、最大値を取る。

\begin{aligned}R_{1}(R_{2}+R)+RR_{2}=2R(R_{1}+R_{2})\end{aligned}

\begin{aligned}R=\dfrac{R_{1}R_{2}}{R_{1}+R_{2}}\end{aligned}

･･･だいぶ端折った計算ですが、それでも長くなりました。ただ、安定して解くことはできます。

方法2.相加相乗平均を用いる場合

(4)式を変形すると

\begin{aligned}P&=I_{R}^{2} \\ &=\dfrac{(R_{2}E)^{2}}{\lbrace R(R_{1}+R_{2})^{2}+2(R_{1}+R_{2})R_{1}R_{2}+\dfrac{(R_{1}R_{2})^{2}}{R} \rbrace}\end{aligned}

分母について、\(2(R_{1}+R_{2})R_{1}R_{2}\)の項は変数\(R\)を持たないので定数。

よって、変数\(R\)を含む項に注目し、相加相乗平均により

\begin{aligned}R(R_{1}+R_{2})^{2}=\dfrac{(R_{1}R_{2})^{2}}{R} \end{aligned}

\begin{aligned}R=\dfrac{R_{1}R_{2}}{R_{1}+R_{2}}\end{aligned}

増減表の作成など、大小関係の概念を持たずに解くことができました。

最後に

院試では、コイルやコンデンサも入ったRLC回路が出てくることが多いです。

このため、本記事の内容を使用する場面は限られてきますが、将来の電験三種の試験などに備えて覚えておくと助かる場面が来るかもしれません。