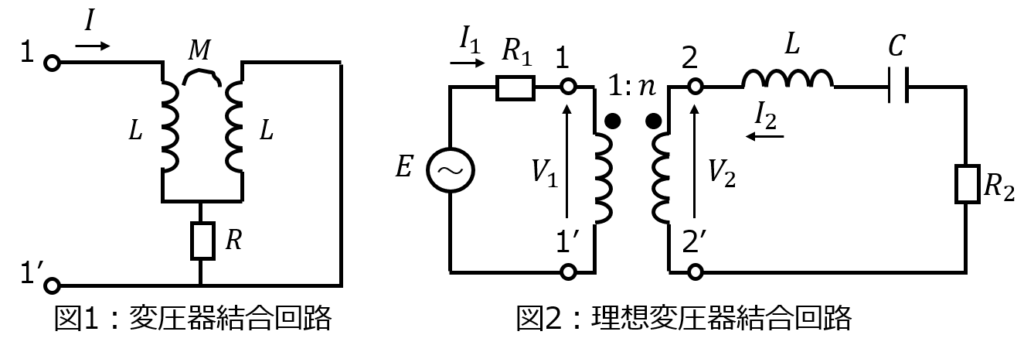
下記の回路について、端子1-1’、端子2-2’から右を見たインピーダンスを求めよ。
(1)相互インダクタンス\(M\)で結合したインダクタンスの下流に抵抗\(R\)を接続した回路。
(2)1次側と2次側の巻き数比が1:nの理想変圧器で結合した回路。
端子から見たインピーダンスの算出方法
見たい方向に電流ベクトル\(I_{in}\)を設定し、その時に発生する電圧\(V_{in}\)の比
\begin{aligned}Z_{in}=\dfrac{V_{1}}{I_{1}}\end{aligned}
で表すことができます。電流を流さなくとも、回路の抵抗、リアクタンスを合成していくだけで求められるケースもあります。しかし、問(2)のような変圧器も含まれた複雑な系の場合はそのように行きません。
結局、電流を仮で設定する上記の方法が最も汎用的な方法となります。
この原則さえ覚えていれば、後は回路の計算を忠実に行うのみです。基本的な知識の組み合わせがモノを言います。
解答例
(1)変圧器結合回路
変圧器結合回路は、T型等価回路に変換できる。
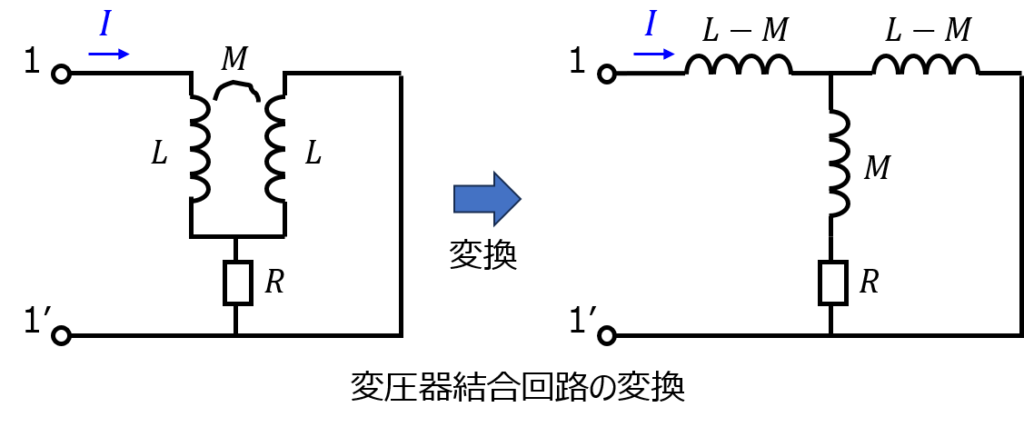
節点aから右を見たインピーダンス\(Z_{a}\)は、並列接続の式を活用すれば良く
\begin{aligned}Z_{a}&=\dfrac{j \omega(L-M)(R+j \omega M)}{R+j \omega M+j \omega (L-M)} \\ &=\dfrac{- \omega^{2}M(L-M)+j \omega R(L-M)}{R+j \omega L}\end{aligned}
よって、端子1-1’にかかる電圧\(V_{1}\)は一番左のインダクタL-M分を考慮すれば良く
\begin{aligned}V_{1}=j \omega(L-M)I_{1}+\dfrac{- \omega^{2}M(L-M)+j \omega R(L-M)}{R+j \omega L}I_{1}\end{aligned}
以上より、端子1-1’から見たインピーダンス\(Z_{1}=\dfrac{V_{1}}{I_{1}}\)は
\begin{aligned}Z_{1}=j \omega(L-M)+\dfrac{- \omega^{2}M(L-M)+j \omega R(L-M)}{R+j \omega L}\end{aligned}
(2)理想変圧器
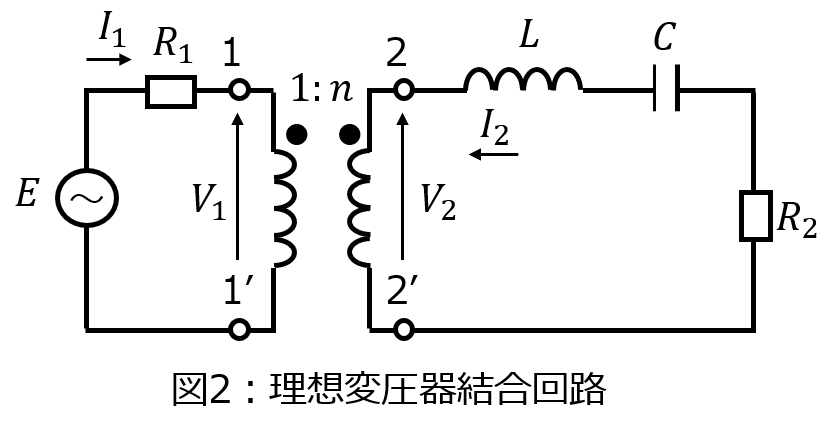
まず、2次側の回路方程式について
\begin{aligned}V_{2}+R_{2}I_{2}+j \omega L I_{2}+\dfrac{I_{2}}{j \omega C}=0\end{aligned}
理想変圧器の式
\begin{cases}nV_{1}=V_{2} \\ I_{1}+nI_{2}=0\end{cases}
を上記の式に代入すると
\begin{aligned}V_{1}=\dfrac{1}{n^{2}}\left(R_{2}I_{1}+j \omega L I_{1}+\dfrac{I_{1}}{j \omega C}\right)\end{aligned}
よって、端子1-1’間のインピーダンス\(Z_{1}\)は、上式に\(I_{1}\)を除すれば良く
\begin{aligned}Z_{1}=\dfrac{1}{n^{2}}\left(R_{2}+j \omega L +\dfrac{1}{j \omega C}\right)\end{aligned}
参考文献
大学課程 電気回路(1) 第3版 大野 克郎,西 哲生(共著) 第6章