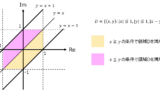【電気通信大学】情報理工学研究科 情報ネットワーク工学専攻 (情報学専攻) 院試対策 必須科目(線形代数、微分積分)

試験範囲

必須科目は、数学です。線形代数、微分積分からなります。

全体としては標準的な難易度ですが、一部電通大特有の問題があります。

本記事は、情報ネットワーク工学専攻の対策を中心に記載します。情報学専攻も、同様の試験範囲ですが、情報ネットワーク工学専攻に対し一部の問題が省略されています。

電通大 情報理工学研究科 情報ネットワーク工学専攻 院試の全体

必須科目、選択科目で分かれています。選択科目は、電気系の科目から情報系の科目の計8科目で構成されています。

選択の幅が広く、大問ごとの難易度差はあまり無いです。全体として、7,8割取れれば人気研究室を除いて第一志望を狙えると考えます。

1科目にかけられる時間は45分です。分量に対して適切な時間だと思います。

線形代数は、基底と次元が頻出です。ただし、固有値を用いた多項式の計算が出題される年もあります。

本サイトでは、様々な線形代数の記事を取り上げています。下記の記事が特に対策に役立つと思います。

解析学については、重積分と極値の計算が毎年出題されます。

重積分は、積分範囲を絞る。極値は、2階微分してからの関係を注意深く見ることが重要です。

下記の記事が対策になると思います。

補足：情報学専攻の場合

出題範囲としては同じです。ただし、情報ネットワーク工学専攻の問題から一部省略されています。

大問の最後の問を省略していることが多いです。情報ネットワーク工学専攻の問題に対し、簡単になっています。

満点も狙える内容と思います。

全体

最近3年分は以下の分野の出題がありました。

線形代数について、冒頭で述べた通りです。基底と次元は、他大学の院試ではあまり出題されないのに対し、電通大では超頻出です。問題集で必ず演習しましょう。

微分積分について、区分求積やマクローリン展開が出題された年もあります。重積分と極値の勉強が完了したら、追加で対策しましょう。

情報学専攻も同じ範囲の出題です。情報ネットワーク工学専攻と同じ対策をすれば良いと思います。

教科書

基本的に、市販の演習書を網羅的に練習していくと良いです。院試向けの本など、難しい内容にまで手を出す必要は無いと考えます。

線形代数

一般的な大学では教養科目に属するため、シラバスが曖昧で指定教科書は無いです。しかし、電通大の場合はシラバスがありました。単科大学だからでしょうか。

線形代数学講義(増補版) 木田 雅成 (著) (シラバス対象本)

シラバスでは増補版前の記載のままになっているかもしれませんが、2024年7月現在の最新版を紹介します。

内容は薄めですが、定理などの基本的な解説がしっかりしています。

また増補版では、複素数と内積の関係についても述べられているようです。実数だけでなく、複素数を成分として有する行列が今後出題される可能性もあります。

よっぽどの理由が無ければ、増補版を購入するのをオススメします。

演習 線形代数 寺田 文行 (著)

本演習書で広く浅く練習することで、傾向違いの出題にあたったとしても十分合格点を取り得る知識が身につくでしょう。

基底と次元、多項式の計算について重点的に取り組み、表現行列などの終盤の章は例題のみの勉強で良いと思います。

解析学

同じくシラバスがありました。指定教科書の紹介をしたのち、管理人がオススメする本を紹介します。

入門微分積分 三宅 敏恒 (著) (シラバス対象本)

薄い本なので、短期間で演習できます。それでいて、頻出分野の極値と重積分はそれなりの分量と難易度で説明しています。

まさに電通大対策が出来る本です。オススメです。

欠点は、演習問題が略解だけなことです。大変痛いですが、例題だけでも練習する価値はあります。

解析演習 (数学演習ライブラリ 2) 野本 久夫 (著), 岸 正倫 (著)

あとは問題集で広く浅く対策していくことをオススメします。本書に限らず、広い範囲をカバーしている本をオススメします。

大学院入試専用の難しい本にまで手を出す必要はないと思います。

対策に使える他大学の問題

電通大の問題は、基底と次元の分野を中心に独自色が強いです。

ですので、下記でオススメはしようと思いますが、優先度としては下げて頂いて問題無いと思います。

線形代数は、出題される大学を紹介するに留めておきます。一押しはありません。

解析学は、農工大が似ていると思います。極値の計算、重積分ともに同じ経路の問題が出題されます。類題演習に使えると考えます。