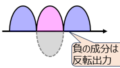
(1)図1に示すΔ型三相交流不平衡回路に線間電圧200Vの対称三相電圧を加える。各相の相電流を求めよ。ただし、\(V_{ab}\)の位相を基準とし、各相のインピーダンスはそれぞれ、5Ω、10Ω、20Ωとする。
(2)図2のように、各層の線間電圧100Vの三相交流回路に\(Z_{1}=10,Z_{b}=4+j3,Z_{c}=3-j4\)の不平衡負荷をY型に接続する。電圧側と中性点を結んだ時、中性点に流れる電流\(I_{N}\)を求めよ。
不平衡三相交流回路とは
三相交流の各相の負荷が等しくない回路を言います。各相が等しい場合は平衡三相交流回路と言い、1相分の電流、電圧、電力を求めれば、それを3倍するだけで全体の特性が分かりました。
一方で、不平衡の場合は、特性が異なるため単純に3倍することはできず、相毎に計算する必要があります。そのため、一般的にこちらの方が問題を解くことが難しいです。
そこで、本記事では不平衡三相交流回路を解くために必要な知識を順に説明していきます。まずは、簡単な例として平衡負荷の場合からやります。
平衡三相交流回路の計算
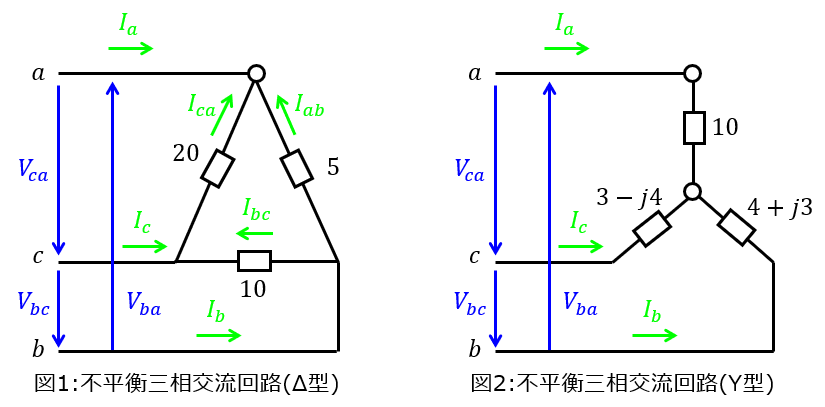
よくある問題パターンとして、負荷に流れる電流を求める問題です。下記のような電気回路を考えます。
電圧はY型に対し負荷側はΔ型なので、このままでは計算が難しいです。負荷側をΔ-Y変換し、インピーダンスを書き直すと\(Z\)になります。
三相全て対称のため、1相分の電流を求めれば、それが他の相に対しても同じになります。(ただし、位相は120度ずつ進むか遅れる。)
\begin{aligned}I=\dfrac{V_{a}}{Z}\end{aligned}
電力に関しても同じです。1相分の3倍なので
\begin{aligned}P=3V_{a}I\end{aligned}
ただし、\(V_{a}=V_{b}=V_{c}\)です。
不平衡三相Δ型交流回路の計算
各相に流れる電流を地道に計算していけば良いです。
下記のように、線間電圧\(V_{ab},V_{bc},V_{ca}\)をΔ型の負荷\(Z_{ab},Z_{bc},Z_{ca}\)に接続した回路を考えます。
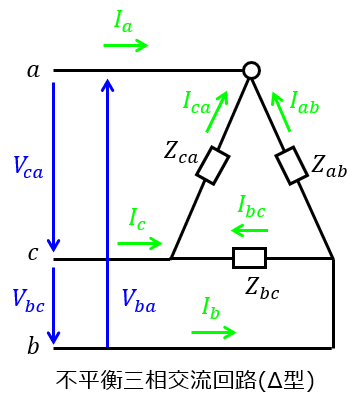
電源側も同じΔ型ですので、各相に流れる電流は、各相の線間電圧と負荷をオームの法則に基づいて解けば良く
\begin{cases}I_{ab}=\dfrac{V_{ab}}{Z_{ab}} \\ I_{bc}=\dfrac{V_{bc}}{Z_{bc}}\end{cases}
線電流に関しては、ベクトル合成により下記の関係になります。
\begin{cases}I_{a}=I_{ab}-I_{ca} \\ I_{b}=I_{bc}-I_{ab} \\ I_{c}=I_{ca}-I_{bc}\end{cases}
このように、1相分の結果を単純に3倍できないですが、計算としては単純なものになります。
不平衡三相Y型交流回路の計算
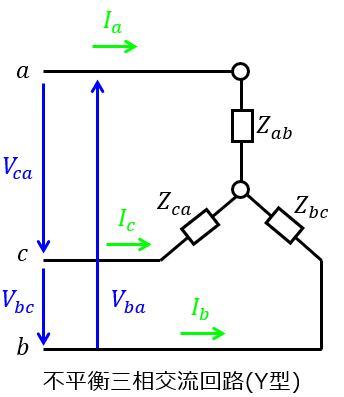
Δ型の電圧に対し、Y型のインピーダンスを接続している場合も考えます。そもそも、Y型の負荷をΔ変換し、前節の解き方をした方が楽な場合が多いですが、あえてこのまま解いてみます。
まず、Y型の中性点について、キルヒホッフの電流則により
\begin{aligned}I_{a}+I_{b}+I_{c}=0\end{aligned}
各線間電圧において、電圧則により
\begin{cases}V_{ab}=Z_{a}I_{a}-Z_{b}I_{b} \\ V_{bc}=Z_{b}I_{b}-Z_{c}I_{c}\end{cases}
()式に()式を代入すると
\begin{aligned}V_{bc}=Z_{b}I_{b}-Z_{c}(-I_{a}-I_{b}) \\ I_{b}=\dfrac{V_{bc}-Z_{c}I_{a}}{Z_{b}+Z_{c}}\end{aligned}
上式を(5)の第1式に代入し
\begin{aligned}V_{ab}=Z_{a}I_{a}-Z_{b}\dfrac{V_{bc}-Z_{c}I_{a}}{Z_{b}+Z_{c}}\end{aligned}
\begin{aligned}I_{a}=\dfrac{Z_{c}V_{ab}+Z_{b}(V_{ab}+V_{bc})}{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}\end{aligned}
線間電圧の和を全て足し合わせると0になるので
\begin{aligned}V_{ab}+V_{bc}+V_{ca}=0\end{aligned}
(9)式を(8)式に代入し
\begin{aligned}I_{a}=I_{a}=\dfrac{Z_{c}V_{ab}-Z_{b}V_{ca}}{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}\end{aligned}
同様に、添え字aをb、cに、bをc,aに、cをa,bに置き換えると
\begin{aligned}I_{b}=I_{a}=\dfrac{Z_{a}V_{bc}-Z_{c}V_{ab}}{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}\end{aligned}
\begin{aligned}I_{b}=I_{a}=\dfrac{Z_{a}V_{bc}-Z_{c}V_{ab}}{Z_{a}Z_{b}+Z_{b}Z_{c}+Z_{c}Z_{a}}\end{aligned}
を得る。このように、不平衡負荷においても、各相に対しオームの法則を適用し、電流と電圧の和が0である性質を利用することで各相に流れる電流値を求められます。
解答例
(1)各相の相電流
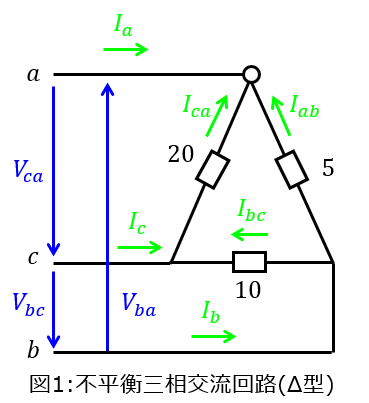
各相の線間電圧は、\(V_{ab}\)を基準とすると、下記のようになる。
\begin{cases}V_{ab}=200 \\ V_{bc}=200e^{-j 2\pi/3}=-100-j100\sqrt{3} \\ V_{ca}=200e^{j 2\pi/3}=-100+j100\sqrt{3}\end{cases}
よって、各相の線電流は
\begin{cases}I_{ab}=\dfrac{V_{ab}}{5}=40 \\ I_{bc}=\dfrac{V_{bc}}{10}=-10-j10\sqrt{3} \\ I_{ca}=\dfrac{V_{bc}}{20}=-5-j5\sqrt{3}\end{cases}
相電流に直すと、ベクトルの性質により
\begin{cases}I_{a}=I_{ab}-I_{ca}=45-j5\sqrt{3} \\ I_{b}=I_{bc}-I_{ab}=-50-j10\sqrt{3} \\ I_{c}=I_{ca}-I_{bc}=5+j15\sqrt{3}\end{cases}
(2)中性点に流れる電流
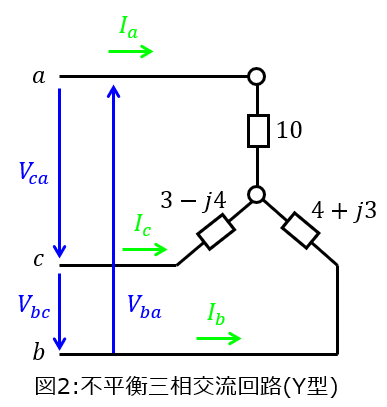
相電圧は\(\frac{100}{\sqrt{3}}\)なので、各相に流れる相電流は
\begin{cases}I_{a}=\dfrac{100}{10\sqrt{3}}=5.77 \\ I_{b}=\dfrac{100e^{-j2\pi/3}}{(4+j3)\sqrt{3}}=-\dfrac{4}{\sqrt{3}}(2+\dfrac{3\sqrt{3}}{2}-j 1.5+j2 \sqrt{3})=-10.61- j 4.54 \\ I_{c}=\dfrac{100e^{j2\pi/3}}{(3-j4)\sqrt{3}}=\dfrac{4}{\sqrt{3}}(-1.5-2\sqrt{3}+j\dfrac{3}{2}\sqrt{3}-j2)=-11.46+j1.38 \end{cases}
中性点に流れる電流\(I_{N}\)は、
\begin{aligned}I_{N}&=I_{a}+I_{b}+I_{c} \\ &=-16.3-j3.16\end{aligned}
最後に
不平衡負荷の場合でも、各相毎に電流を考えることで解けることが分かりました。本問が解ければ、院試問題でも臆することなく立ち向かうことができます。