院試でよく使う電気回路の基本事項まとめ

はじめに

本記事は、院試に向けた電気回路の基本事項のまとめ記事になります。電磁気学のまとめ記事も過去に紹介しましたが、兄弟記事になります。

インダクタ、キャパシタを虚数(フェーザ表示)で表して、後は高校数学と同じ計算をすることが多いですが、大問の後半には、テブナンの定理や供給電力最大則を利用した問題がよく問われます。この部分が大学電気回路特有で、知識として持っておく必要があります。

なお、過渡現象に関しては微分方程式を解くことに尽きます。ラプラス変換を用いて解くことが多いですが、必要な公式について、こちらの記事で解説しています。

本記事では、フェーザ回路に関する重要事項を主にまとめます。

電気回路の重要公式

重要度大

これは覚えておかないと、電気回路の勉強がままならないレベルです。初学者の方はもちろん、すぐに反応出来なかった方は必ず覚えましょう。

並列回路の公式

インピーダンス$Z_1$,$Z_2$を並列接続している回路の合成インピーダンス$Z$は

$$\begin{array}{}\text{(1)}& \begin{array}{r}Z={\displaystyle \frac{Z_1{Z}_2}{Z_1+Z_2}}\end{array}\end{array}$$

高校物理でよく出てくる並列回路の公式

$$\begin{array}{}\text{(2)}& \begin{array}{r}{\displaystyle \frac{1}{Z}}={\displaystyle \frac{1}{Z_1}}+{\displaystyle \frac{1}{Z_2}}\end{array}\end{array}$$

は、左辺が逆数なので計算にひと手間要ります。これをすぐ使える形に変形したのが(1式)ですね。大学の教科書では(2式)を断りなく使われることが多いですが、上記の背景になっています。

(1式)、(2式)ともに抵抗だけでなく、虚部を含むインピーダンスにも適用できます。

アドミタンス$Y$

インピーダンス$Z$を逆数に取ったものです。

前章で並列回路の合成インピーダンスを考えましたが、合成アドミタンスは下記になります。

$$\begin{array}{}\text{(3)}& \begin{array}{r}Y=Y_1+Y_2\end{array}\end{array}$$

(2式)の各項の逆数をそのまま取れば良いので上式のようになります。共振周波数を求める問題の時、使うことがあります。インピーダンスの虚部=0を与える周波数が共振周波数になりますが、アドミタンスの虚部=0で考えても同じ結果が得られるためです。

並列回路の場合、アドミタンスを用いて解くことも視野に入れましょう。

フェーザ表示

正弦波$v(t)=\sqrt{2}\sin (\omega t+\varphi )$のフェーザ表示は基準位相に応じて下記のようになります。

• $\sin (\omega t)$を基準位相とする場合：$v(t)\sim e^{\varphi }$
• $\cos (\omega t)$を基準位相とする場合：$\sin (\omega t+\varphi )=\cos (\omega t-\pi /2+\varphi )$より、$v(t)\sim e^{-j\frac{\pi }{2}+\varphi }$

基準位相に三角関数(sin,cos)を合わせ、瞬時値の振幅を√2で割って表現します。下記に示すインダクタンスとコンデンサのフェーザ表示を覚えておけば事足りることが多いですが、大学によっては上記の式をフェーザ表示で表すことを最初に問うことがあります。(電通大など)

上記の大学を志望する方は今一度確認しておきましょう。

コイル、コンデンサのフェーザ表示

$e^{j\omega t}$の時間微分は$j\omega e^{j\omega t}$、積分は$\frac{1}{(j\omega }$の項が付くことから、それぞれ下記になります。

$$\begin{array}{}\text{(4)}& \{\begin{array}{l}\mathrm{イ}\mathrm{ン}\mathrm{ダ}\mathrm{ク}\mathrm{タ}\mathrm{ン}\mathrm{ス}：j\omega L\\ \mathrm{キ}\mathrm{ャ}\mathrm{パ}\mathrm{シ}\mathrm{タ}\mathrm{ン}\mathrm{ス}：{\displaystyle \frac{1}{j\omega C}}\end{array}\end{array}$$

各大学の院試において、必ず出てくる最頻出事項です。必ず覚えましょう。

共振周波数(共振角周波数)

与えられたインピーダンス回路の虚部が0になる周波数を言います。例えば、RLC直列回路のインピーダンスは

$$\begin{array}{}\text{(5)}& \begin{array}{r}Z=R+j\omega L+{\displaystyle \frac{1}{j\omega C}}\end{array}\end{array}$$

ですが、虚部=0を考えると、$\omega =\frac{1}{\sqrt{LC}}$になります。インダクタンス成分とコンデンサ成分が打ち消し合っています。この時の電流が最大になることから、共振周波数の成分の信号をよく通すことが分かります。このことから、ラジオの選局、フィルタとして使用されます。

複素電力、有効電力、無効電力

電圧ベクトルと電流ベクトルの複素共役の積を複素電力と言います。

$$\begin{array}{}\text{(6)}& \begin{array}{r}S=\mathit{V}･\overline{\mathit{I}}\end{array}\end{array}$$

上式を計算した結果の実部が有効電力、虚部が無効電力に対応します。

有効電力については、高校物理の式$P=R{I}^2$でも求められますが、無効電力も問われている際は、複素電力を使った方が一石二鳥です。

変圧器

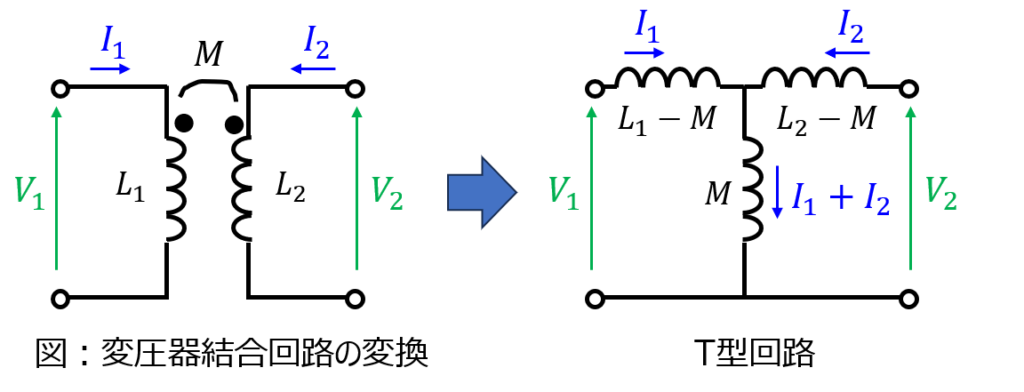
相互インダクタンス$M$で結合している変圧器(一次側のインダクタンス$L_1$、二次側のインダクタンスは、下記の回路方程式になります。

これを変形し、T型回路のように表すこともできます。二端子対回路で問われることもあります。予備知識としてどうぞ。

理想変圧器の場合

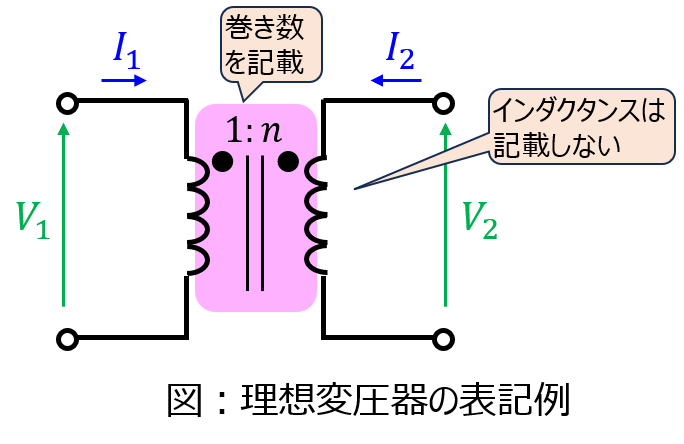
巻き数比1:nの理想変圧器が接続されている場合は下記の関係式になります。

$$\begin{array}{}\text{(7)}& \{\begin{array}{l}n{V}_1=V_2\\ I_1+n{I}_2=0\end{array}\end{array}$$

相互インダクタンスの概念が無くなり、純粋に巻き数比で考えれば良い式になります。問題文では、どちらが問われているのか、必ずチェックしましょう。

重要度中

重要度大では、これを覚えておけば、何とか電気回路の計算ができる。くらいのレベルのものを話しました。ですが、実際はこれだけでは足りません。

二端子対回路など、複雑な回路が問われることもあります。本章では、二端子対回路を中心に重要事項を話していきます。

テブナンの定理

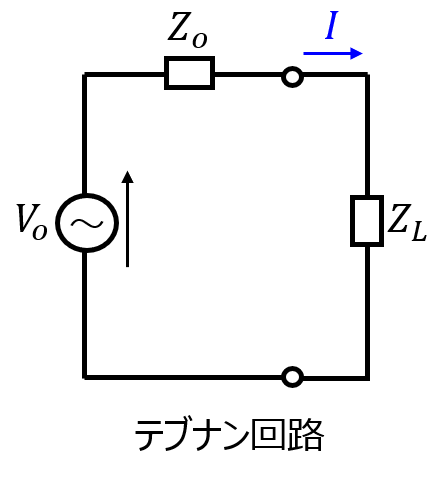
注目している端子間の開放電圧が$V_o$、端子間から回路を見たインピーダンスを$Z_o$とします。あるインピーダンス$Z_L$を接続した時に流れる電流$I$は下記のようになります。

$$\begin{array}{}\text{(8)}& \begin{array}{r}I={\displaystyle \frac{V_o}{Z_o+Z_L}}\end{array}\end{array}$$

電圧源から回路を見るのではなく、端子間から回路を見たときのインピーダンス$Z$を求めることに注意しましょう。

ノートンの定理

注目している端子間の短絡電流を$I_s$、端子から回路を見たアドミタンスを$Y_o$、接続する負荷のアドミタンスを$Y_L$とすると、端子間の電圧$V$は下記で示されます。

$$\begin{array}{}\text{(9)}& \begin{array}{r}V={\displaystyle \frac{I_s}{Y_o+Y_L}}\end{array}\end{array}$$

テブナンの定理と双対になっています。問題文で、端子間に流れる電流、電圧、どちらが問われているのかを確認しましょう。

供給電力最大則

インピーダンスが$Z=A+jB$の回路に負荷インピーダンス$Z_o$を接続する時、

$$\begin{array}{}\text{(10)}& \begin{array}{r}{Z}_o=\overline{Z}\end{array}\end{array}$$

のように、複素共役の場合、実部が等しく、虚部が打ち消し合うため、負荷の消費電力が最大になります。(負荷の実部が小さすぎると、負荷の消費電力が小さくなるが、大きすぎると回路に流れる電流が小さくなるので、その塩梅が等しい実部の条件ってことですね。)

Z行列、Y行列、F行列

回路の一次側の電流、電圧をそれぞれ下記になります。

$$\begin{array}{}\text{(11)}& \begin{array}{r}\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{cc}{z}_{11}& z_{12}\\ z_{21}& z_{22}\end{array}\right)\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)\end{array}\end{array}$$

$$\begin{array}{}\text{(12)}& \begin{array}{r}\left(\begin{array}{c}{I}_1\\ I_2\end{array}\right)=\left(\begin{array}{cc}{y}_{11}& y_{12}\\ y_{21}& y_{22}\end{array}\right)\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)\end{array}\end{array}$$

$$\begin{array}{}\text{(13)}& \begin{array}{r}\left(\begin{array}{c}{V}_1\\ I_1\end{array}\right)=\left(\begin{array}{cc}{f}_{11}& f_{12}\\ f_{21}& f_{22}\end{array}\right)\left(\begin{array}{c}{V}_2\\ I_2\end{array}\right)\end{array}\end{array}$$

Z行列の場合は、回路の一次側、二次側を開放してZ行列の各成分を求める。Y行列の場合は短絡して各成分を求める。F行列の場合は両方やる。という基本解法になります。

フィルタ

ざっくりとですが、二次側にコンデンサがある回路は積分回路、一次側にある場合は微分回路になります。要は、二次側の素子が一次側の素子より積分項が強ければ積分回路、弱ければ微分回路になります。周波数特性を図示する問題も出てきますので、対策しておきましょう。

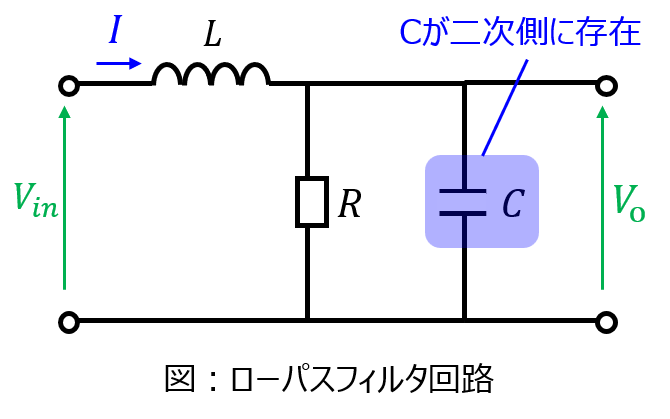
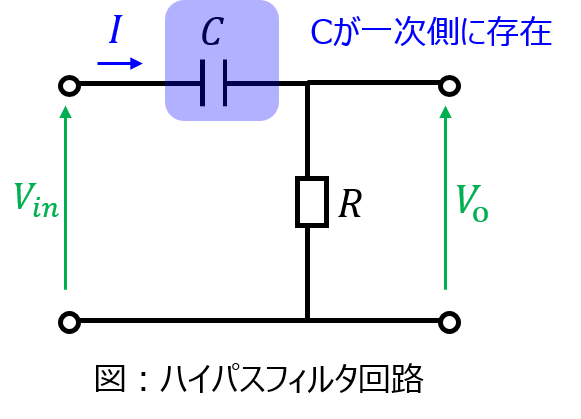
重要度小

重要度中である程度の問題に太刀打ちできるようになりますが、大学によっては分布定数回路などが出題されることがあります。

本章では、一部の大学を対策する上で覚えておきたい事項を紹介します。

ベクトル軌跡

与えられたパラメータのある文字を変数とし、0から∞まで変化させたときの軌跡を複素平面上にプロットしたものです。

RC並列回路におけるインピーダンス$Z$について、$\omega$を0から∞に変化した場合の軌跡

$$\begin{array}{}\text{(14)}& \begin{array}{r}Z={\displaystyle \frac{R}{1+j\omega CR}}\end{array}\end{array}$$

を考えます。分数をそのまま考えると大変なので、分母、分子を個別に変化させることを考えて、最後に組み合わせる思考方法だと、プロットしやすいです。

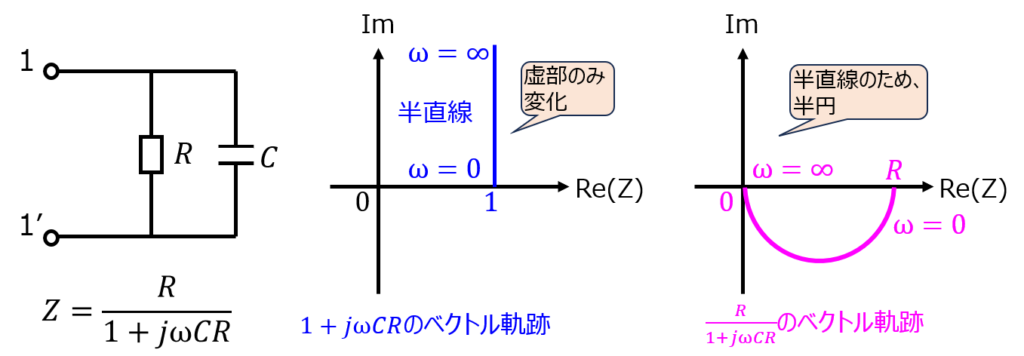
分布定数回路の基本式

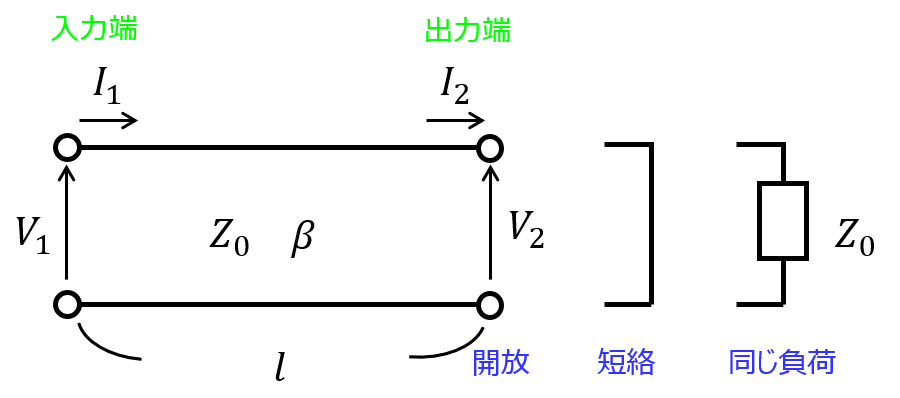
無損失線路の場合、出力端からx離れた場所の電圧、下記になります。

$$\begin{array}{}\text{(15)}& \{\begin{array}{l}{V}_1=V_2\cos \beta l+j{Z}_0{I}_2\sin \beta l\\ I_1=j\frac{V_2}{Z_0}\sin \beta l+I_2\cos \beta l\end{array}\end{array}$$

二端子対回路のF行列と同じ表し方をできますので、二次側を短絡、開放、別の負荷$Z$を接続したときは、都度、二次側のパラメータに$V_2=0,I_2=0,V_2=Z{I}_2$を代入して上式を整理しましょう。

最後に

本基本事項と合わせて演習をし、自分の理解を育てていきましょう。