2024年1月 | 電気情報の森

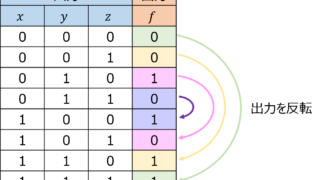
【論理関数】n変数対称関数、多数決関数の性質

論理関数

f_{1} (x_{1}, x_{2}, \dots, x_{i}, \dots, x_{j}, \dots x_{n})

の

x_{i}, x_{j}

を入れ替えた関数

f_{2} (x_{1}, x_{2}, \dots, x_{j}, \dots, x_{i}, \dots x_{n})

の

x_{i}, x_{j}

を考える。任意の

i, j

について

f_{1}, f_{2}

の出力が等しいとき、n変数対称関数と言う。

2024.01.31

情報

npnバイポーラトランジスタの動作原理。特性向上のための方策と制約

npnバイポーラトランジスタの動作原理をバンド図を使用して説明せよ。また、特性を向上させるための施策、制約について述べよ。npnバイポーラトランジスタに関する問題は、論述形式で出題されることが多いです。本記事も、論述ベースで作成していきます。

2024.01.30

半導体デバイス

電磁波の性質と導出、基本問題の解法パターン

透過、反射に関する問題も出てきますが、基本的にマクスウェル方程式を解くことで解決するパターンが多いです。電場(E)が未知数の場合、式(2)の第1式に磁場Hを代入し、計算する。磁場(H)が未知数の場合、式(2)の第2式に電場Eを代入し、計算する。

2024.01.29

通信

【分布定数回路】スミスチャートを利用した問題

スミスチャートとは反射係数の式を利用し、ある位置における駆動点インピーダンスを複雑な計算無しで求められるよう図式化したものです。取りうる全てのインピーダンスを反射係数に変換して、単位円内に表示したものになります。

2024.01.28

通信

【分布定数回路】出力端を開放、短絡したときの過渡現象の問題

下図のように(a) 入力端に特性インピーダンス

Z_{0}

を接続した分布定数回路(b) 入力端にインピーダンスが存在しない分布定数回路を考える。電圧源Eを入力端に接続し、出力端を(i)開放、(ii)短絡する。

0 ≦ x ≦ l

の範囲における電圧、電流の時間変化を(a)(b)の場合それぞれ求めよ。ただし、伝搬速度を

v

とする。

2024.01.27

通信

同じ積分計算をフーリエ変換、ラプラス変換それぞれの方法で解く

(1)複素積分の考え方を利用し、下記の積分値を求めよ。

\begin{array}{r} (1) & \int_{0}^{\infty} \frac{\cos t x}{1 + x^{2}} d x \end{array}

ただし、積分路は下記(図1)を採用すること。

2024.01.25

数学

【論理関数】n変数線形関数の個数、性質

あるn変数論理関数について、

\begin{array}{r} (2) & f (x_{1}, x_{2}, \dots, x_{n}) = c_{0} \oplus c_{1} x_{1} \oplus c_{2} x_{2} \oplus \dots \oplus c_{n} x_{n} \end{array}

が成立するとき、線形関数と呼ぶ。

2024.01.24

情報

半導体のバンド構造、フェルミ準位まとめ

伝導帯の有効状態密度を

N_{c}

、価電子帯の有効状態密度を

N_{v}

とすると、ある温度で伝導帯に励起される電子の密度

n

と正孔の密度

p

は、以下のようになる。

\begin{matrix} (3) & {\begin{cases} n = N_{c} \exp (- \frac{E_{c} - E_{f}}{k T}) \\ p = N_{v} \exp (- \frac{E_{f} - E_{v}}{k T}) \end{cases} \end{matrix}

2024.01.22

半導体デバイス

【電磁気学】円環電流と磁気モーメントの等価関係

【問題】下記の導体が総電荷

Q

で一様に帯電している。中心軸周りに一定の角速度

ω

で回転するとき、(1)(2)それぞれの場合の磁気モーメントを求めよ。(1)半径

a

長さ

b

の円柱導体(2)半径

a

の導体球

2024.01.20

電磁気学

【論理関数】n変数自己双対関数の個数、性質

論理関数の性質に関する問題は、東北大を初め、京大などで出題されます。閾値関数、対称関数、正関数など、様々な関数が存在しますが、本問ではまず自己双対関数の性質について例題を用いて説明していきます。

2024.01.17

情報

2024-01