 大阪大学
大阪大学 【大阪大学大学院】工学研究科 電気電子情報通信専攻 基礎科目(電気電子回路)の対策
電気回路について、問題の難易度自体は高いわけでは無いですが、計算量が非常に多いです。特に、文字ではなく具体的な値を代入して結果を求める形式であることから、ただ結果を求めて終わりというわけではありません。最後までしっかり値を求めないと点が取れません。
 大阪大学
大阪大学  大阪大学
大阪大学  大阪大学
大阪大学 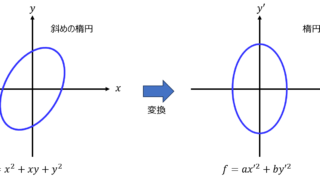 数学
数学  数学
数学  京都大学
京都大学 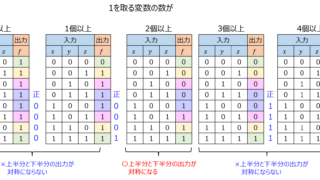 情報
情報