ストークスの定理を用いたベクトル場の面積分問題

ストークスの定理とは

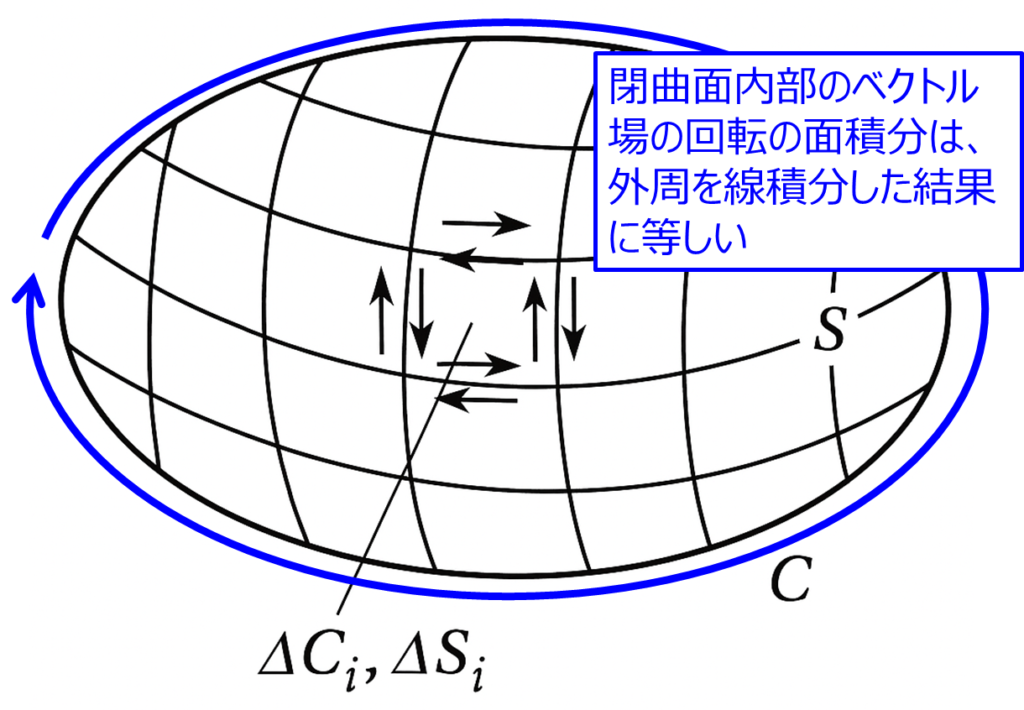
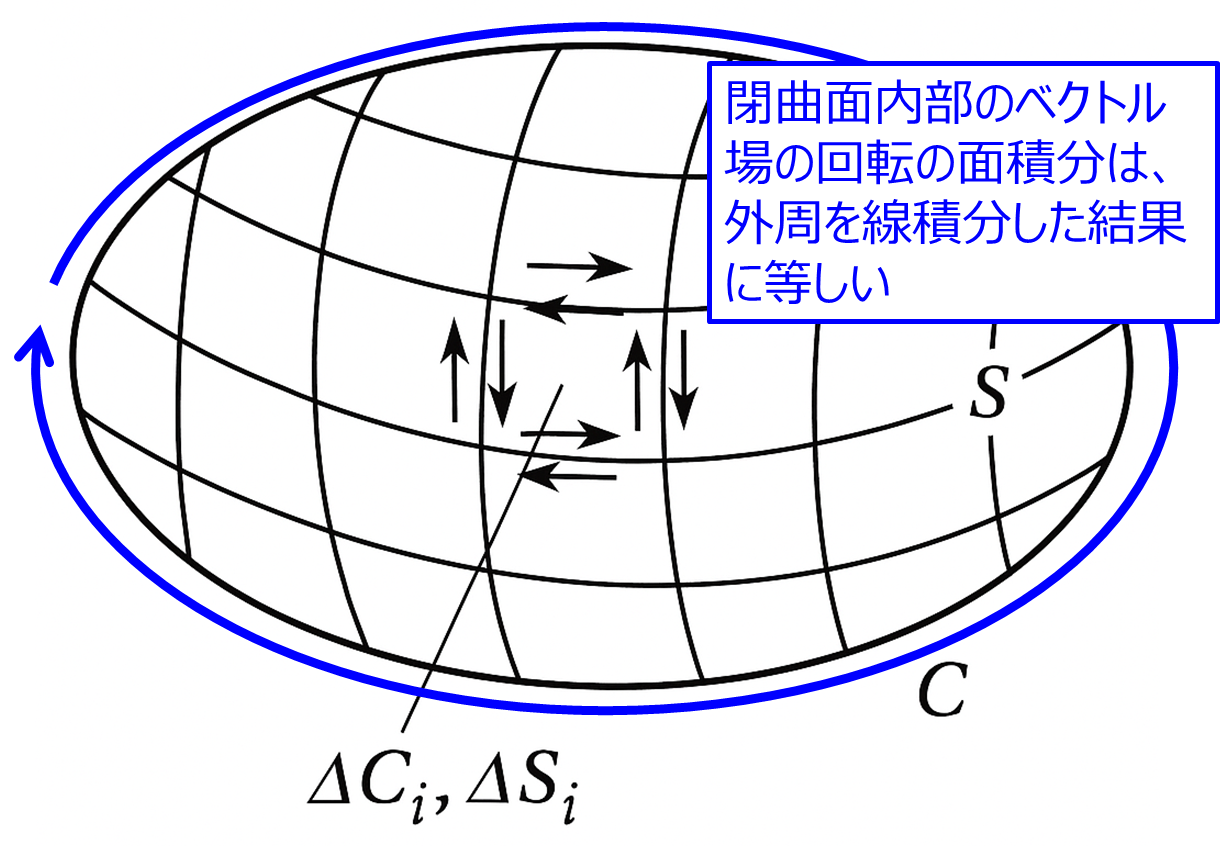
あるベクトル場の回転の面積分は、面積分した領域の境界線を線積分した値に等しいことを言います。下記の計算式で表されます。

\begin{aligned}\int_{S} (\Delta \times \boldsymbol{A}) \cdot d\boldsymbol{S}=\int_{c} \boldsymbol{A} \cdot d\boldsymbol{r}\end{aligned}

本問も線積分の式で表されていますが、ストークスの定理を用いることで面積分に帰着できます。問で与えられた領域に対し面積分すれば解けます。(逆にした方が解きやすい場合もあるので臨機応変に考えましょう)

電磁気学におけるストークスの定理

よく、変動磁場による誘導起電力の関係を理解するために用います。

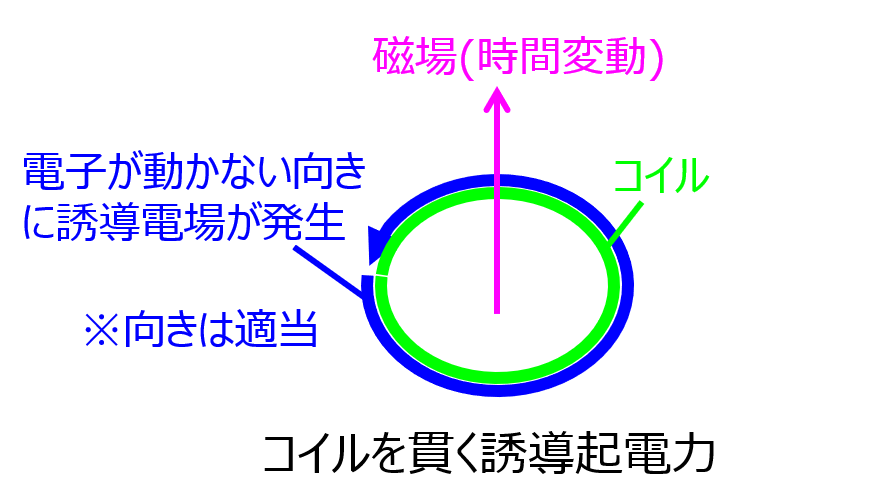
あるコイルの閉曲面Sを貫く磁場の誘導起電力\(V\)は、磁束\(\phi\)の時間微分により、下記の式で表されます。

\begin{aligned}V&=-\dfrac{d\phi}{dt} \\ &=-\dfrac{d}{dt}\int_{s}\boldsymbol{B} \cdot d\boldsymbol{S}\end{aligned}

誘導起電力はコイルの円環に対して発生するわけですから、コイル内に誘導電場$\boldsymbol{E}$が生じていると考えられます。これをコイルの形状に対して線積分し

\begin{aligned}V=\int_{c}\boldsymbol{E} \cdot d\boldsymbol{s}\end{aligned}

なお、Cは閉曲線を表し、コイルの形状となります。上式同士を連立させると

\begin{aligned}-\dfrac{d}{dt}\int_{s}\boldsymbol{B} \cdot d\boldsymbol{S}=\int_{c}\boldsymbol{E} \cdot d\boldsymbol{s}\end{aligned}

ここでストークスの定理を右辺に使用することにより

\begin{aligned}-\dfrac{d}{dt}\int_{s}\boldsymbol{B} \cdot d\boldsymbol{S}=\int_{s}rot\boldsymbol{E} \cdot d\boldsymbol{S}\end{aligned}

時間微分を積分項の中に入れると

\begin{aligned}-\int_{s}\dfrac{\partial \boldsymbol{B}}{\partial t} \cdot d\boldsymbol{S}=\int_{s}rot\boldsymbol{E} \cdot d\boldsymbol{S}\end{aligned}

上式から積分項を排除することにより

\begin{aligned}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t}\end{aligned}

マクスウェル方程式(電磁誘導の法則の微分表現)が導かれました。磁束密度$\boldsymbol{B}$の時間変化により、$\boldsymbol{B}$の垂直方向に誘導電界$\boldsymbol{E}$が生じることを表します。

解答例

問題で与えられた式をストークスの定理を用いて変形する。

\begin{aligned}rot\boldsymbol{A}&=\begin{vmatrix}\boldsymbol{\hat{x}} & \boldsymbol{\hat{y}} & \boldsymbol{\hat{z}} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ \cos(y) & x(y-\sin(y)) & z \end{vmatrix} \\ &=(0-0,0-0,y-\sin(y)+\sin(y)) \\ &=(0,0,y)\end{aligned}

Sの単位法線ベクトル\(\boldsymbol{n}\)を考える。Sはxy平面なので

\begin{aligned}\boldsymbol{n}=(0,0,1)\end{aligned}

与えられた積分範囲は、\(-1 \leqq x \leqq 1,0 \leqq y \leqq \sqrt{1-x^{2}}\)で表されるので

\begin{aligned}\int_{c} \boldsymbol{A} \cdot d\boldsymbol{r}&=\int_{S} (\Delta \times \boldsymbol{A}) \cdot \boldsymbol{n}dS \\ &=\int_{S}(0,0,y) \cdot (0,0,1) dS \\ &=\int^{1}_{-1}dx \int^{\sqrt{1-x^{2}}}_{0}y dy \\ &=\dfrac{1}{2}\int^{1}_{-1}(1-x^{2})dx \\ &=\dfrac{1}{2} \left[x-\dfrac{x^{3}}{3}\right]^{1}_{-1} \\ &=\dfrac{1}{2}\left(2-\dfrac{2}{3}\right) \\ &=\dfrac{2}{3} \end{aligned}

最後に

本問は、数学のベクトル解析の試験で問われることが多いです。しかし、電磁気学しか選択しないという方でも、基本事項を抑えるという意味で有用だと考えられます。