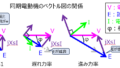
問1:下記のように、地上から2mの高さに光源A,Bが存在し、それぞれの光度を200cd、100cdとする。点P,M,Qの水平面照度を求めよ。なお、点Mは線分PQの中点とする。
問2:200cdの光度を持つ等方的な電球を用いて、半径2mの円を照らすことを考える。全光束の50%が有効に使用されるとしたときの平均照度を求めよ。
問3:幅1.5m、長さ4.0mで反射率が40%の白色の紙に600lmの光束が均一に入射する。このとき、紙から発する反射光の光束発散度を求めよ。
はじめに
照明に関する授業は、大学課程の中でも限られた専攻のだいぶ後半の講義でしか出てきません。そのため、学生時代は選択しておらず、社会人になって電験の勉強をする時に初めて勉強する人も多いと思います。
日常に溢れているので得点しやすいのかと思いきや、見慣れない用語が多く、覚えることが多いです。そのため、意外と得点しにくい科目になります。
捨てても良いのですが、照明に関する問題が2問出てくる年もあります。全体の10%を占める得点配分です。選択問題のときは逃げることもできますが、1問くらいは取っておきたいです。
そこで本記事では、最低限覚えておきたいことを抜粋しました。室係数など照明設計に関する問題は省きますが、それ以外の分野が出てこれば、得点できるのに役立つ内容がつまっています。
照明に関するパラメータ
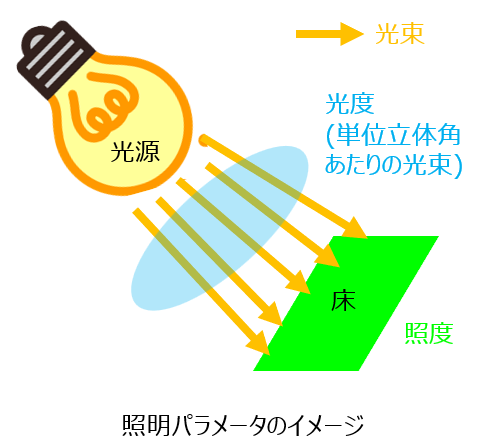
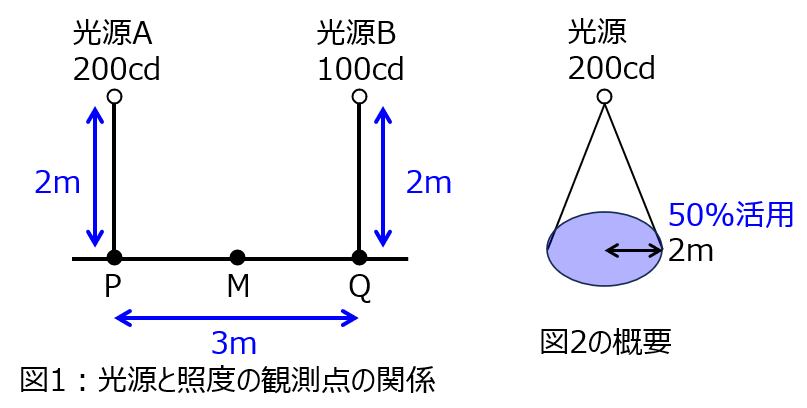
前提:光源、光束
光を発するものを光源と言います。光源から発するエネルギーを放射束と言い、可視光線範囲の放射束を視覚的に測定した量を光束\(F\)(単位:ルーメン)と言います。
光束を起点とし、下記のパラメータがあります。
光度
- 点光源が「特定の方向」にどれだけ強く光を出しているか
ある方向に向かって出される単位立体角あたりの光束を光度と言います。変数として\(I\)で表すことが多いです。(単位:カンデラcd)
つまるところ、方向あたりの明るさを言います。実例として、LEDや懐中電灯の光の鋭さを表します。
照度
- 面がどれだけ明るく照らされているかを表す
ある面に入射する単位面積あたりの光束を言います。変数として\(E\)で表すことが多いです。(単位:ルクス)
教室の机の上の明るさや道路照明の設計で使用します。
照度の光度の関係式
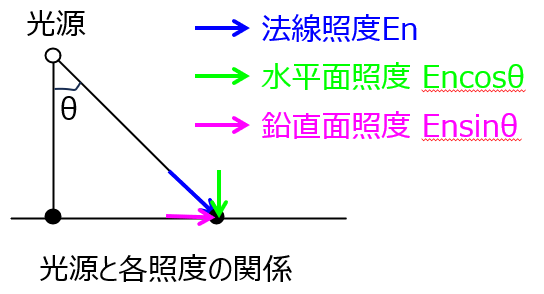
点光源の照度を\(I\)、照度を考える面までの距離を\(r\)とすると
- 法線照度\(E_{n}\):\(E_{n}=\frac{I}{r^{2}}\)
- 水平面照度\(E_{h}\):\(E_{h}=E_{n}\cos \theta\)
- 円直面照度\(E_{v}\):\(E_{h}=E_{n}\sin \theta\)
ベクトル図で表すと上図のようになります。\(E_{h}\)について、水平面と考えるからには地面に対しての接線成分で照度を求めるのかと思いきや、法線成分で考えます。これは、照度の定義から地面を照らす明るさを考えるので法線成分で考える必要があるからです。
また、\(E_{n}\)については、距離\(r\)の-2乗で考えます。-1乗では無いので注意してください。イメージ論ですが、ガウスの法則で球型の閉曲面を取る時も-2乗でした。光束も電束も同じものとして考えるならば-2乗で考える意味もしっくり来るかもしれません。
上記の関係式は、試験で頻出になっています。必ず覚えておきましょう。
補足
上記に比べると出題頻度が落ちますが、知っておいた方が良い事項を2つ紹介します。
補足1:光束発散度と輝度
光源が発光面を持っている時の単位長さあたりの光束を、光束発散度\(M\)と言います。全光束を\(F\)、発光面積を\(A\)とすると、下記で表されます。(単位:lx/m2)
\begin{aligned}M=\dfrac{F}{A}\end{aligned}
また、物体を一定方向から見た時、その物体に垂直な単位面積当たりの明るさを輝度と言います。光度を\(I\)、観測面からの物体の正射影面積を\(A\)とすると、下記で表されます。(単位:cd/m2)
\begin{aligned}L=\dfrac{I}{A}\end{aligned}
照度と似たような計算をしますが、重要なのは光源に注目したパラメータであることです。照度は照らす面の面積で議論していましたが、光束発散度、輝度は光源の面積に注目したパラメータです。
上記2つのパラメータを求める際は、光源の面積をセットで考える癖を付けましょう。
補足2:光波の波長と見える色について
高校物理でも出てきますが、波長が長い順から下記の見え方をします。
| 色 | 紫 | 青 | 緑 | 黄 | 橙 | 赤 |
| 波長域[nm] | 380~430 | 430~490 | 490~550 | 550~590 | 590~640 | 640~770 |
逆からですが、赤橙黄緑青白色(せきとうおうりょくせいはくしょく)と覚えましょう。何かと唱えやすく、少年漫画の必殺技みたいですね。(幽●白書の 邪●炎殺黒龍波的な。)
紫が白になっていますが、覚えやすさを重視しています。万が一紫がどこの波長帯か忘れたときも、青の近くにあるので推測できます。
また、赤と青、どっちが長い波長側なのかド忘れすることがあります。この時、日常生活の日中と夕暮れを思い出すと推測することができます。
- 日中は、太陽と地球の距離が近い。➡波長が短い色でも地球に届く。青色!
- 夕暮は、太陽と地球の距離が長い。➡波長が長い色しか地球に届かない。赤色!
上記のように考えれば良いです。これは、波動の散乱の性質に基づいています。波長が短いほど、目的地まで伝搬する最中に障害物に遮られて届かなくなってしまいますが、短ければ届きます。
解答例
問1:水平面照度
まず、光源Aに関する点P,Q,Mの水平面照度を考える。(単位はルクス lx)
- 点Pまでの長さ:2m
- 点Qまでの長さ:√(2^2+3^2)=√13m
- 点Mまでの長さ:√(2^2+1.5^2)=√6.25=2.5m
cos成分も考えると、
- 点P:θ=0のため、cosθ=1
- 点Q:cosθ=2/√13
- 点M:cosθ=2/2.5
以上より、各点における水平面照度は、単位[lx]で
- 点P:\(E_{hap}=\dfrac{200}{2^{2}}*1=50\)
- 点Q:\(E_{haq}=\dfrac{200}{13}*\dfrac{2}{\sqrt{13}}=8.5\)
- 点M:\(E_{ham}=\dfrac{200}{13}*\dfrac{2}{2.5}=25.6\)
次に、光源Bについても同じことをする。対称性より、距離、cosについては点PとQを光源Aと逆にすれば良い。求める水平面照度は、単位[lx]で
- 点P:\(E_{hbp}=\dfrac{100}{13}*\dfrac{2}{\sqrt{13}}=4.3\)
- 点Q:\(E_{hbq}=\dfrac{100}{13}*1=25\)
- 点M:\(E_{hbm}=\dfrac{100}{2^{2}}*\dfrac{2}{2.5}=12.8\)
上記を足し算すれば良く、求める全体の水平面照度は、単位[lx]とし
- 点P:\(E_{hbp}=54.3\)
- 点Q:\(E_{hbq}=\dfrac{100}{13}*1=33.5\)
- 点M:\(E_{hbm}=\dfrac{100}{2^{2}}*\dfrac{2}{2.5}=38.4\)
問2:平均照度
まず、全光束\(F_{o}\)を考える。球の立体角は4πなので
\begin{aligned}F_{o}=4\pi I=800\pi\end{aligned}
全光束の50%が半径2mの円を照らすので、求める平均照度は、単位[lx]とし
\begin{aligned}E&=\dfrac{800 \pi *0.5}{\pi *2^{2}} \\ &=100[lx]\end{aligned}
問3:光束発散度の計算
余裕があればやってみてください。
光源は、幅1.5m、長さ4.0mの長方形となる。反射率0.4も考慮すると、求める光束発散度は(1)式により
\begin{aligned}M=0.4*\dfrac{600}{1.5*4}=40[lm/m2]\end{aligned}