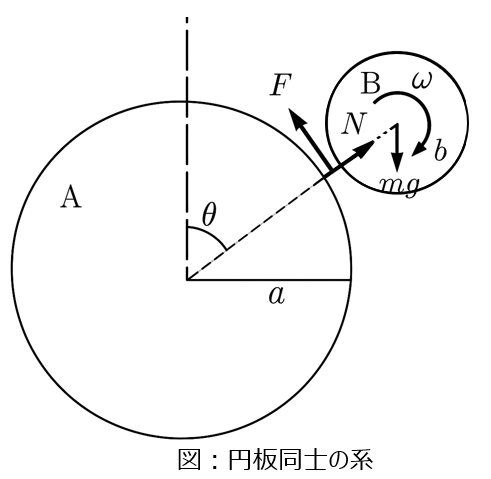
下記のように、半径\(a\)、質量\(M\)の円筒Aの上に半径\(b\)、質量\(m\)の円筒Bを置く。時計回りに微小な力を加えると、円筒Bは初速0で転がりだした。円筒Bが受ける摩擦力を\(F\)、垂直抗力を\(N\)とし、下記の問いに答えよ。なお、重力加速度gと鉛直方向と円筒の中心をなす角\(\theta\)を解答として用いて良い。
問1:円筒Bについて、接線方向の運動方程式を求めよ。
問2:円筒Bについて、鉛直方向の運動方程式を求めよ。
問3:円筒Bについて、回転に関する運動方程式を求めよ。
はじめに
大学入試の力学と大学に入ってからの力学の大きな違いの一つに、回転方向の運動方程式を扱うことがあります。問1,2のような、物体がどこかへ動く場合の運動方程式の左辺は質量\(m\)で扱うことに対し、回転方向の運動方程式は慣性モーメント\(I\)を使用します。
回転方向の運動方程式
トルクを\(T\)として、下記で表されます。
\begin{aligned}I\dfrac{d^{2} \theta}{dt^{2}}=T\end{aligned}
右辺はトルクで考えます。単に、質点にかかる力\(F\)で考えるわけではないので注意しましょう。この事実は問(3)で使用します。
慣性モーメント\(I\)の性質
電気系にとっては聞き慣れない言葉かもしれませんが、物体の回転運動の変化しにくさを表す物理量をいいます。
直線方向の運動方程式で言う、質量\(m\)と同じイメージを持てば良いです。
質量\(m\)が大きいほど、ある力\(F\)をかけても加速しにくいですが、慣性モーメントも大きいほど回転しづらい振る舞いになります。
一方で、減速時においては質量\(m\)が大きいほど減速しづらく、慣性モーメントについても回転数が落ちづらくなります。
慣性モーメントの求め方
物体の形状によって異なりますが、代表的な2つを紹介します。
半径\(a\)、質量\(m\)の質点、剛体それぞれ下記になる。
- 質点:\(I=mr^{2}\)
- 剛体:\(I=\int^{a}_{0}r^{2}dm\)
半径の2乗がキーになります。質点の場合は、質量に対しそのまま乗算するだけで良いです。剛体の場合は、微小半径\(dr\)に含まれる質量\(dm\)を区間[0,a]に対し面積分すれば良いです。下記の式で表されます。
\begin{aligned}dm=\dfrac{m}{\pi a^{2}}r^{2}dr\cdot r d\theta\end{aligned}
分母分子の項は密度を表し、\(dr \cdot rd \theta\)は区間\(dr\)の微小断面積を表します。円筒導体の電場の面積分と同じ考え方ですね。ガウスの法則を適用するときの式と似ていると気づいた方もいるかもしれません。
電気系における使用場面
同期発電機の安定性について考える場面で使用します。発電機の出力\(P_{m}\)と負荷側の消費\(P_{e}\)の差により、トルクの変化が発生。この時、慣性モーメントの大きさによって発電周波数の偏差の大小が決まります。
詳しくはこちらの記事で解説しています。慣性モーメントに対する本記事を読んだ後に見てみると、より理解が進むでしょう。
解答例
問1:接線方向の運動方程式
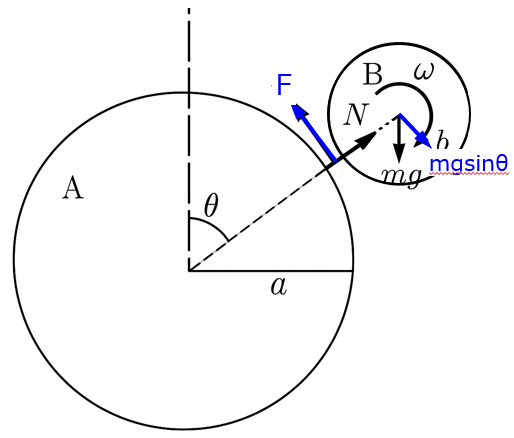
基本は運動方程式を立式するだけですが、座標変換だけ一工夫要ります。接線方向は、物体の\(\theta\)方向に力を及ぼすため
\begin{aligned}m\dfrac{dv}{dt}=mg \sin \theta-F\end{aligned}
\(v=r \omega, \omega=\frac{d \theta}{dt},r=(a+b)\)を用いると
\begin{aligned}m(a+b)\dfrac{d^{2}\theta}{dt^{2}}=mg \sin \theta-F\end{aligned}
問2:法線方向の運動方程式
問1と同様にして立式する。中心方向の加速度は\(\frac{v^{2}}{r}\)で表されるので
\begin{aligned}m\dfrac{v^{2}}{r}=mg \cos \theta -N \end{aligned}
\(v=r \omega,r=a+b\)より
\begin{aligned}m(a+b)\left(\dfrac{d\theta}{dt}\right)^{2}=mg \cos \theta -N\end{aligned}
問3:回転方向の運動方程式
前章で紹介したように、まず慣性モーメント\(I\)を求める。\(dm\)は(1)式で表される。半径が\(b\)であることに注意して
\begin{aligned}I&=\int^{2 \pi}_{0}\int^{b}_{0}\dfrac{m}\pi b^{2}r^{2}rdr d \theta \\ &=2\pi \dfrac{m}{\pi b^{2}}\left \lbrack\dfrac{r^{4}}{4}\right\rbrack^{b}_{0} \\ &=\dfrac{mb^{2}}{2}\end{aligned}
トルク\(T\)は\(T=Fb\)で表されるので、求める運動方程式は
\begin{aligned}\dfrac{mb^{2}}{2}\left(\dfrac{d \theta}{dt}\right)^{2}=Fb\end{aligned}
最後に
機械系出身者ではなくとも、一般教養として必要な知識が詰まっています。問題は解けなくても、前章で説明した慣性モーメントのイメージくらいは覚えておきましょう。