【数値解析】台形積分の性質と誤差の説明と例題

情報

2025.10.02

台形積分を用いて、\begin{aligned}s=8\int^{2}_{1}\dfrac{1}{x}dx\end{aligned}を小数点以下第3桁まで求めよ。ただし、刻み幅は$h=\frac{1}{4}$とする。
電気通信大学 2019年8月情報ネットワーク系院試専門科目7 数値計算(1)(b)より引用

台形積分とは
1. 台形積分の誤差評価
  1. 導出：局所的誤差
  2. 導出：全体誤差
解答例
最後に

台形積分とは

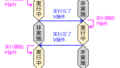
数値積分において、積分区間を台形で分割し、近似して和を取る方法です。計算機(コンピュータ)を用いて積分する際、よく用いられる方法です。

イメージ図を下記に示します。ある一変数関数$f(x)$が与えられているとします。この関数は複雑な式になっており、手計算で求められないとします。このとき、長方形型の短冊$[x_{i},x_{i+1}]$で積分区間を区切って、結果を足し合わせていく方法があります。しかし、この方法は曲線の部分で誤差が発生します。

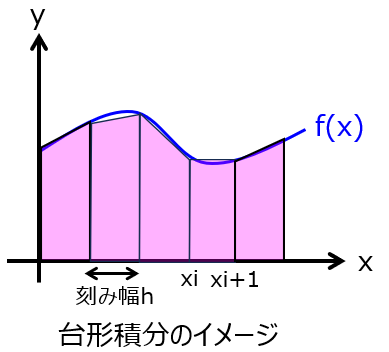
台形積分の場合、曲線で変化する部分も一次近似することができ、誤差を低減できます。$x_{i},f(x_{i})$に隣接する点$x_{i+1}=x_{i}+h$の値$f(x_{i+1})$が分かれば、下記になります。

\begin{aligned}S_{i}=\dfrac{h}{2}\left ( f(x_{i})+f(x_{i+1})\right)\end{aligned}

一区間分の計算結果を他区間でも足し合わせていけば良いので、全体の積分結果$S$は下記のようになります。

\begin{aligned}S&=\sum^{n}_{i=1}S_{i} \\ &=\dfrac{h}{2}\left ( f(a)+2\sum^{n-1}_{k=1}f(a+kh)+f(b)\right)\end{aligned}

台形積分の誤差評価

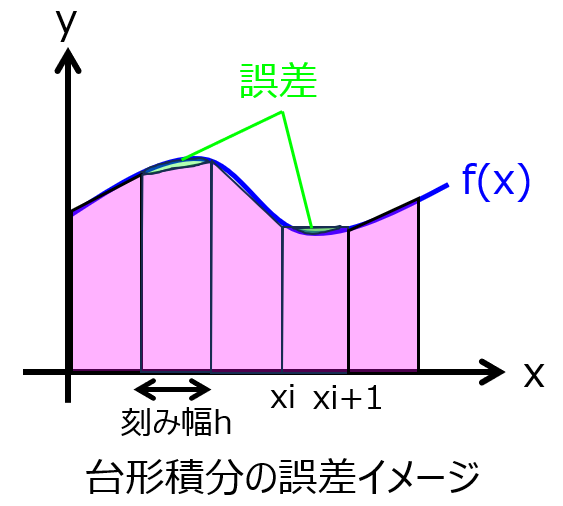
台形積分は一次近似ですので、曲線状の関数の場合、どうしても誤差が発生します。刻み幅$h$に対し、どのように影響するのでしょうか。

まず結論ですが、下記になります。

局所的な近似誤差：$O(h^{3})$ 刻み幅の3乗
全体的な近似誤差：$O(h^{2})$ 刻み幅の2乗

導出：局所的誤差

誤差関数$E$を、真値と近似式の差を取り、下記のように定義します。

\begin{aligned}E=\int^{a+h}_{a}f(x)dx-\dfrac{h}{2}\left ( f(x_{i})+f(x_{i+1})\right)\end{aligned}

積分項は、テイラー展開(5式)を用いて下記のように近似できます。

\begin{aligned}f(a+h) = f(a) + h f'(a) + \frac{h^2}{2} f”(a) + \frac{h^3}{6} f^{(3)}(\xi_1), \quad \xi_1 \in (a,a+h)\end{aligned}

\begin{aligned}\int_a^{a+h} f(x)\,dx &= \int_0^h \Big( f(a) + t f'(a) + \frac{t^2}{2} f”(a) + \cdots \Big)\ dt \\ &= f(a)h + \frac{h^2}{2} f'(a) + \frac{h^3}{6} f”(a) + \frac{h^4}{24} f^{(3)}(\xi_2), \quad \xi_2 \in (a,a+h). \end{aligned}

\begin{aligned} \frac{h}{2}\big[ f(a) + f(a+h) \big] &= \frac{h}{2}\Big[ f(a) + f(a) + h f'(a) + \frac{h^2}{2} f”(a) + \frac{h^3}{6} f^{(3)}(\xi_1) \Big] \\ &= h f(a) + \frac{h^2}{2} f'(a) + \frac{h^3}{4} f”(a) + \frac{h^4}{12} f^{(3)}(\xi_1). \end{aligned}

(4式)に(6式)、(7式)を代入し、3次以下の項を無視すると下記になります。

\begin{aligned} E &= \Big( \frac{h^3}{6} – \frac{h^3}{4} \Big) f”(a) + \text{高次項} \\
&= -\frac{h^3}{12} f”(\xi), \quad \xi \in (a,a+h).
\end{aligned}

$h^{3}$で表されるので、オーダー3乗ですね。