確率変数の積率母関数と最尤推定値の計算問題

ある感染症の発症間隔を確率変数\(X\)とする。確率変数\(X\)はパラメータ\(\lambda\)を持つ下記の確率密度変数に従うものとする。

\begin{aligned}f(x)=\beta^{2}xe^{-\beta x}\end{aligned}

問1：確率変数\(X\)の積率母関数\(\phi(\theta)=E[e^{\theta X}]\)を求めよ。
問2：\(X\)の期待値\(E[X]\)および分散\(V[X]\)を求めよ。
問3：n個の標本\(X_{1},X_{2},\cdots,X_{n}\)が独立に(1)式の分布に従うとする。これらの標本値を\(x_{1},x_{2},\cdots,x_{n}\)とするとき、パラメータ\(\lambda\)の最尤推定値\(\hat{\lambda}\)を求めよ。

電気通信大学 2021年8月実施 院試問題 確率統計より抜粋

はじめに

積率母関数、最尤推定値は、電気情報系の学生からするとあまり馴染みのない概念かもしれませんが、電通大など、特定の大学の院試で問われることがあります。

積率母関数については、知っておくと期待値と分散の計算が以前の記事で紹介した方法より楽にできる場合があります。別の大学を受ける方でも、問1,2の解答例は覗いておくと、試験本番で役立つかもしれません。

パラメータの説明

積率母関数

確率分布のモーメントを生成する関数で、確率分布の性質を評価するために使用します。

期待値\(E\)の変数を指数関数とし、下記で表します。

\begin{cases}\phi(\theta)=E[e^{x\theta}] \\ E[e^{x\theta}]=\int^{\infty}_{-\infty}e^{x\theta }f(x)dx\end{cases}

なお、\(f(x)\)は与えられた確率密度関数です。積率母関数を\(\theta\)で微分し、0を代入することを考えます。微分の回数ごとに下記の関係があります。

1階微分と2階微分はよく使います。期待値や分散を求める材料になることから、院試問題として出題しやすいです。必ず覚えましょう。

最尤推定値とは

観測データが最も起こりやすくなるパラメータを言います。本問で与えられた確率密度関数\(f(x)=\lambda^{2}xe^{-\beta x}\)を例にして考えます。

この関数の確率密度に応じて、データ\(x_{1},x_{2},\cdots,x_{n}\)が得られたとします。そのデータが得られる確率を尤度と言い、これを最大化する\(\beta\)が最尤推定値となります。

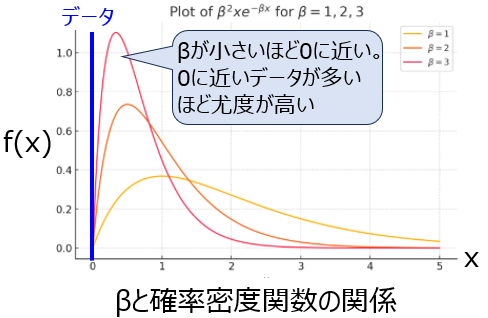
例えば、データ\(x_{1},x_{2},\cdots,x_{n}\)が全て\(x=0\)付近で得られたとしましょう。(上図の青線部分)
\(f(x)\)は\(\beta\)の値に依存しますが、\(\beta=1\)の場合、確率密度関数のピークが0に近いため、\(\beta=2,3\)に対して尤度の高いパラメータだと推察できます。

結局、最尤推定値は、尤度関数\(L\)に対して下記の関係を与える\(\beta\)で求められます。

\begin{cases}L(x_{1},x_{2},\cdots,x_{n}, \beta )=\prod^{n}_{i=1} f(x_{i}) \\ \dfrac{\partial L}{\partial \beta}=0\end{cases}

データ\(x_{1},x_{2},x_{n}\)をそれぞれ含む確率密度関数の積項を目的変数\(\beta\)で偏微分し、0を与える\(\beta\)を計算すれば良いわけですね。

解答例

問1：積率母関数\(\phi(\theta)\)の算出

(2)式を用いると、求める\(\phi(\theta)\)は

\begin{aligned}\phi(\theta)&=\int^{\theta}_{0}e^{\theta x}\cdot \beta^{2}xe^{-\beta x}dx \end{aligned}

\(t=-(\beta-\theta)x\)に変数変換すると、積分範囲は[0,-∞]になる。また、\(\dfrac{dt}{dx}=-\beta+\theta\)なので

\begin{aligned}\phi(\theta)&=\dfrac{\beta^{2}}{-(\beta-\theta)}\int^{-\infty}_{0} \dfrac{t}{-(\beta-\theta)}e^{t}dt \\ &=\dfrac{\beta^{2}}{(\beta-\theta)^{2}} \left \lbrack te^{t} \right \rbrack ^{-\infty}_{0}- \dfrac{\beta^{2}}{(\beta-\theta)^{2}}\int^{-\infty}_{0}e^{t}dt \\ &=\dfrac{\beta^{2}}{(\beta-\theta)^{2}}\end{aligned}

問2 期待値と分散

前章の説明より、問1で求めた積率母関数\(\phi(\theta)\)を1階微分、2階微分し、\(E[X],E[X^{2}]\)を求める。

\begin{aligned}\phi'(\theta)&=-\beta^{2}\cdot -2 \dfrac{1}{(\beta-\theta)^{3}} \\ &=\dfrac{2 \beta^{2}}{(\beta-\theta)^{3}}\end{aligned}

\begin{aligned}E[X]=\phi'(0)=\dfrac{2}{\beta}\end{aligned}

\begin{aligned}\phi^{\prime \prime}(0)&=2\beta^{2}\cdot3\dfrac{(\beta-\theta)^{2}}{(\beta-\theta)^{6}} \\ &=\dfrac{6 \beta^{2}}{(\beta-\theta)^{4}}\end{aligned}

\begin{aligned}E[X^{2}]=\phi^{\prime \prime}(0)=\dfrac{6}{\beta^{2}}\end{aligned}

以上より、求める分散\(V[X]\)は

\begin{aligned}V[X]&=E[X^{2}]-E[X] \\ &=\dfrac{6}{\beta^{2}}-\dfrac{4}{\beta^{2}} \\ &=\dfrac{2}{\beta}\end{aligned}

問3：最尤推定値

尤度関数\(L\)を考える。

\begin{aligned}L&=\beta^{2} \prod^{n}_{i=1}x_{i}e^{-\beta x_{i}} \\ &=(x_{1}x_{2} \cdots x_{n})\beta^{2n}e^{-\beta(x_{1}+x_{2}+\cdots +x_{n})}\end{aligned}

これを\(n\)で偏微分して

\begin{aligned}\dfrac{\partial L}{\partial \beta} &=(x_{1}x_{2}\cdots x_{n})-2n\beta^{2n-1}e^{-\beta(x_{1}+x_{2}+\cdots+x_{n})}\\ & -(x_{1}x_{2}\cdots x_{n})(x_{1}x_{2} \cdots x_{n})\beta^{2n}e^{-\beta(x_{1}+x_{2}+\cdots +x_{n})} \end{aligned}

これを整理して

\begin{aligned}\dfrac{\partial L}{\partial \beta}=(x_{1}x_{2}\cdots x_{n})\beta^{2n-1}e^{-\beta(x_{1}+x_{2}+\cdots+x_{n})}\left \lbrace 2n-\beta(x_{1}+x_{2}+\cdots+x_{n})\right \rbrace\end{aligned}

\(\dfrac{\partial L}{\partial \beta}=0\)より、求める最尤推定値は

\begin{aligned}\beta=\dfrac{2n}{x_{1}+x_{2}+\cdots+x_{n}}\end{aligned}

最後に

最尤推定値の計算は、煩雑になることが多いです。指数が付くことが多いので、logを取った方が楽になる場合があります。結局、=0を与える\(\beta\)を考えれば良いので、logを取ったとしても結果に影響はありません。