振幅\(A\)、周期\(T\)をもつ正弦波信号\(s(t)\)に電力スペクトル密度\(P_{n}(f)\)が\(\frac{N_{o}}{2}\)である信号が重畳された信号\(s_{n}(t)\)を考える。信号\(s_{n}(t)\)は伝達関数\(H(f)\)をもつ帯域幅\(B\)の理想低域フィルタに入力される。\(s(t)\)および\(H(f)\)は次式で与えられる。
\begin{aligned}s(t)=A\sin\left(\dfrac{2 \pi t}{T}\right)\end{aligned}
\begin{aligned}H(f)=\begin{cases}1 \quad |f|≦\frac{B}{2} \\ 0 \quad otherwise \end{cases}\end{aligned}
ただし、\(\frac{B}{2} > \frac{1}{T}\)である。
(1)信号\(s(t)\)の平均電力\(P_{s}\)を求めよ。
東北大学 電気情報系 院試 2021/3月 通信工学 (2)(3)より抜粋
(2)フィルタ出力の雑音の平均電力\(P_{n}\)を求めよ。
(3) (1)(2)を元に、信号対雑音比S/Nを求めよ。
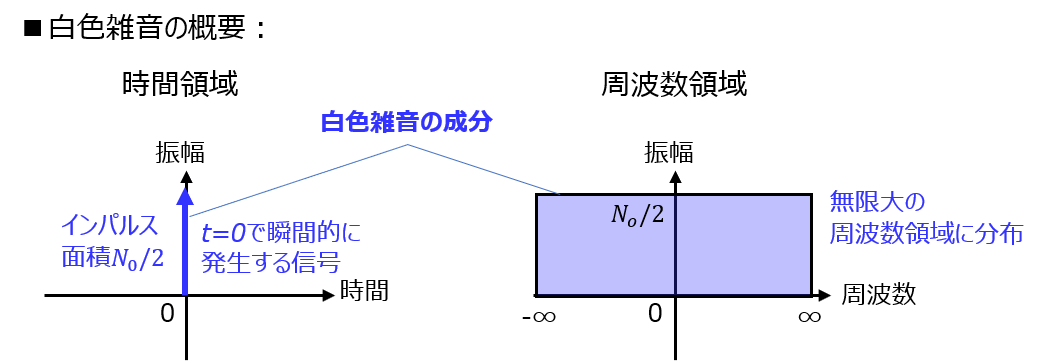
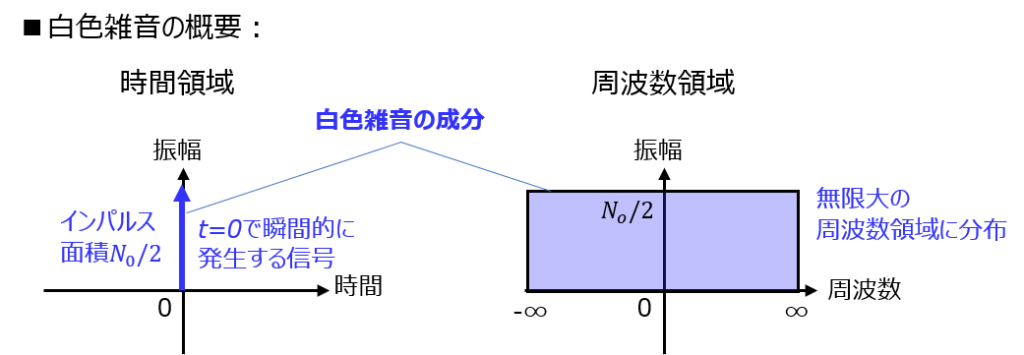
白色雑音とは
電力スペクトル密度\(N(f)\)が全ての周波数で一定の雑音を言います。
時間領域\(t\)に落とし込むとインパルス関数になることから、ある時間で瞬間的に発生した雑音と言い換えることもできます。
SN比とは
入力信号\(s(t)\)から発生する電力\(P_{s}\)に対するノイズの電力\(P_{n}\)の比\(\frac{P_{s}}{P_{n}}\)を言います。
入力信号の平均電力は、信号の2乗を考えれば良く、下記の式で表すことができます。
\begin{aligned}\dfrac{1}{T}\int ^{T }_{0}\left| x\left( t\right) \right| ^{2}dt \end{aligned}
“平均”電力のため、信号を2乗した値を時間\(T\)で割ることを忘れないことが重要です。
ノイズの電力は、時間領域だとインパルス関数で計算できず、周波数領域でも無限に広がっているので、無限大となっています。
このままだとSN比を計算できないですが、こういった時、フィルタがセットで付いてきます。
周波数領域にて、バンド幅-B/2~B/2に制限できますので、結局この面積を計算することで、求めることができます。
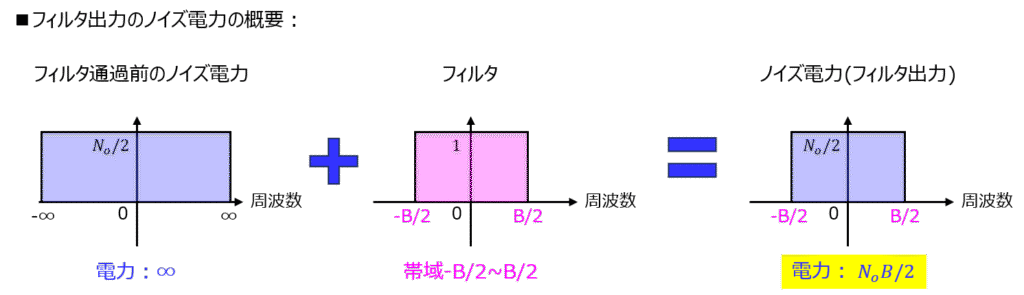
白色雑音のとき、周波数領域では一定値となりますので、ノイズの電力を計算する上では長方形の面積を求めれば良いことになります。
出題者側としては作問がしやすいことから、SN比を求める問題は白色雑音が出てくることが定番です。
解答例
(1)信号の平均電力
信号の平均電力は、(3)式より
\begin{aligned}P_{s}&=\dfrac{1}{T}\int^{T}_{0}A^{2}\sin^{2}\left(\dfrac{2 \pi t}{T}\right)dt \\ &=\dfrac{A^{2}}{T}\left[\dfrac{t}{2}-\dfrac{1}{4}\sin\left(\dfrac{4 \pi t}{T}\right) \right]^{T}_{0} \\ &=\dfrac{A^{2}}{2}\end{aligned}
(2)ノイズの電力
帯域幅Bのフィルタのため
\begin{aligned}P_{n}=\dfrac{N_{o}}{2}B\end{aligned}
(3)SN比の求め方
式(4)(5)の比をとって
\begin{aligned}S/N=\dfrac{A^{2}}{BN_{o}}\end{aligned}
最後に
SN比に関する問題は、通信工学でよく出てきます。
本問の考え方がベースになります。是非マスターしましょう。