直積集合とは
集合\(X,Y\)を構成するそれぞれの要素\((x,y)\)の組全体の集合\(X×Y\)を言います。
論理式では、下記のように表すことができます。
\begin{aligned}X×Y=\lbrace(x,y)|x\in X,y\in Y\rbrace\end{aligned}
(x,y)は順序を区別します。\(x≠y\)ならば、\((x,y)≠(y,x)\)、\(X×Y≠Y×X\)になります。
これは、xはある数値:3、yはただの文字:bで当てはめてみると分かりやすいです。
3bの文字列とb3の文字列は一致しません。ですので、上記の原則が説明できます。
n個の集合を組み合わせた直積集合
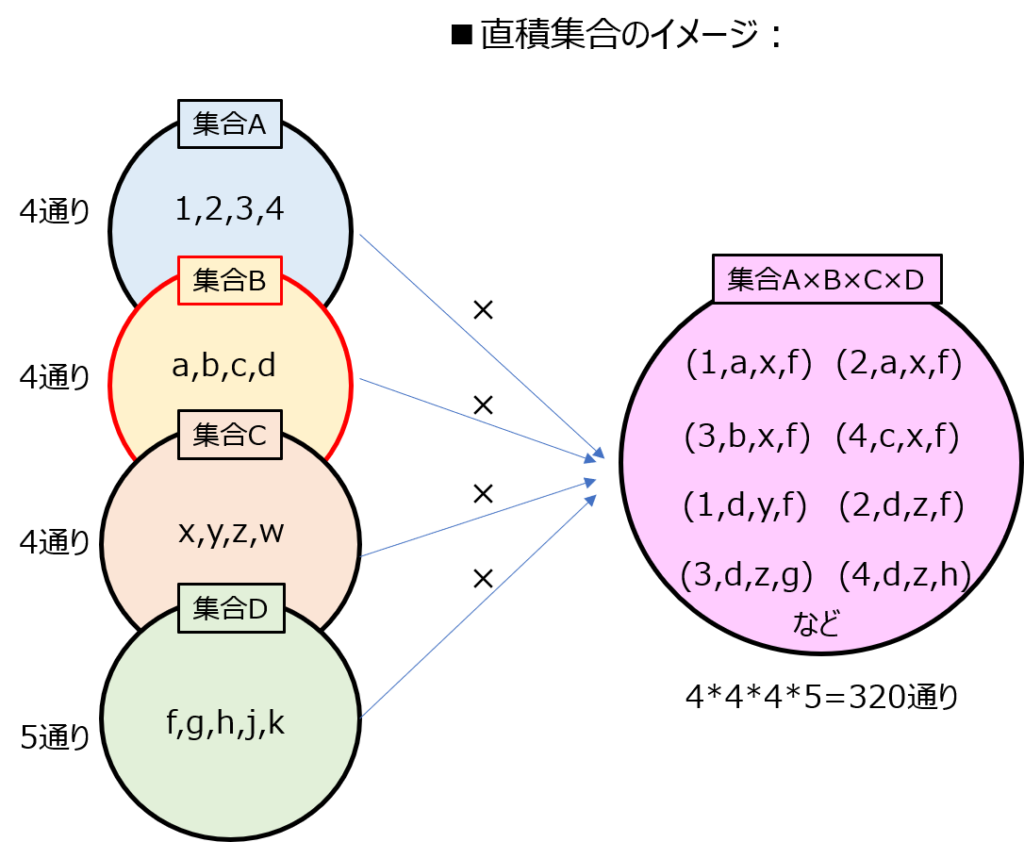
(1)式は、2つの集合の間の関係式を示していましたが、3つ以上の集合に対しても同様に成立します。(下記)
\begin{aligned}X_{0}×X_{1}× \cdots ×X_{n-1}=\lbrace(x_{0},x_{1},\cdots,x_{n-1})|x_{0}\in X_{0},x_{1}\in X_{1},\cdots,x_{n-1}\in X_{n-1}\rbrace\end{aligned}
\(X_{0},X_{1},,\cdots,X_{n-1}\)それぞれの集合を構成する要素数を\(m_{0},m_{1},\cdots,m_{n-1}\)とします。これら全てを組み合わせた直積集合の要素数\(m_{total}\)は
\begin{aligned}m_{total}=\prod ^{n-1}_{i=0}n_{i}\end{aligned}
になります。順序が関係するため、それぞれの集合が持っている要素数を全て掛け合わせると全体の要素数が分かります。
他、ある集合\(X_{i}\)が空集合だった場合、直積集合も空集合になることが分かります。逆に、ある集合\(X_{i}\)が無限集合だった場合、直積集合も無限集合になります。
直積集合の性質
様々な性質がありますが、代表的なものに下記4つがあります。証明付きで説明していきます。
- \(X\subseteq Y \cap Z\subseteq W\)のとき、\(X×Z \subseteq Y×W\)
- \(X×Y \subseteq Z×W\)と\(X\subseteq Z \cup Y\subseteq W\)は同値
- \(X×(Y\cap Z)=(X×Y)\cap (X×Z)\)
- \(X×(Y\cup Z)=(X×Y)\cup (X×Z)\)
\(X\subseteq Y \cap Z\subseteq W\)のとき、\(X×Z\subseteq Y×W\)
ある2つ集合\(X,Z\)それぞれの部分集合\(Y,W\)同士の直積を組み合わせたとき、部分集合同士の直積は、集合同士の直積に属することを示しています。
証明
\(X\)の全ての要素は\(Y\)に属する。また、Zの全ての要素は\(W\)に属する。よって、\(X\)と\(Z\)の直積\(X×Z\)の全ての組み合わせ(x,z)は\(Y\)と\(W\)の直積\(Y×W\)で表現できる。
よって、命題は成立できた。
\(X×Y \subseteq Z×W\)と\(X\subseteq Z \cap Y\subseteq W\)は同値
(左条件式)が成立するとき、(右条件式)も成立する (証明1)
(右条件式)が成立するとき、(左条件式)も成立する (証明2)
を交互に証明し、同値関係を導く。
証明1
\(X×Y \subseteq Z×W\)について、任意の\(x \in X\)、\(y \in Y\)に対して\((x,y) \in X×Y\)
\(X×Y \subseteq Z×W\)より、\((x,y) \in Z×W\)、\(x \in Z, y \in W\)も成立する。
これより、下記の関係が得られる。\begin{aligned}X \subseteq Z \cap Y \subseteq W\end{aligned}
証明2
逆に、\(X\subseteq Z \cup Y\subseteq W\)から始めた場合も同様に証明できる。
任意の\(x \in X\)、\(y \in Y\)に対して\((x,y) \in X×Y\)に対して
\begin{aligned}x \in X \subseteq Z \cap y \in Y \subseteq W\end{aligned}
により、\((x,y) \in Z × W\)が得られる。
以上より、\begin{aligned}X×Y \subseteq Z×W\end{aligned}になる。
(1)式(3)式を互いの式を発端とし、相手の式を証明できたので、同値関係である。
\(X×(Y\cap Z)=(X×Y)\cap (X×Z)\)
\(X×(Y\cap Z) \subseteq (X×Y)\cap (X×Z)\) (証明1)
\(X×(Y\cap Z) \subseteq (X×Y)\cap (X×Z)\) (証明2)
をそれぞれ証明し、両者を満たす等号=の関係を導く。
証明1
一般的に、\(Y \cap Z \subseteq Y, Y \cap Z \subseteq Z \)が成立することに注目する。
\(Y \cap Z \subseteq Y\)に直積Xを組み合わせた場合でも
\begin{aligned}X×(Y \cap Z) \subseteq X × Y \end{aligned}
が成立し、\(Y \cap Z \subseteq Z\)の場合も同様に
\begin{aligned}X×(Y \cap Z) \subseteq X × Z \end{aligned}
が成立する。
直積集合の性質1より、\(X×(Y \cap Z)\)は、\(X × Y ,X × W\)の部分集合としてみると
\begin{aligned}X×(Y\cap Z) \subseteq (X×Y)\cap (X×Z)\end{aligned}
であることが証明できた。
証明2
集合\(X,Y\)それぞれに含まれる要素\(x,y\)を
\begin{aligned}(x,y) \in (X×Y) \subseteq (X × Z)\end{aligned}
とすると、下記2つの関係が導かれる
\begin{cases}(x,y) \in (X × Y) \quad x \in X,y \in Y \\ (x,y) \in (X × Z) \quad x \in X,y \in Z \end{cases}
(11)式より、\begin{aligned}x \in X , y \in Y \subseteq Z\end{aligned}
になるので、\((x,y)\)を組み合わせた直積
\begin{aligned}X×(Y\cap Z) \supseteq (X×Y)\cap (X×Z)\end{aligned}
も成立する。
(9)式(13)式を組み合わせて、題意の式(下記)が証明できた。
\begin{aligned}X×(Y\cap Z)=(X×Y)\cap (X×Z)\end{aligned}
\(X×(Y\cup Z)=(X×Y)\cup (X×Z)\)
大方針としては、一つ前の式の証明と同じです。
\(X×(Y\cap Z) \subseteq (X×Y)\cup (X×Z)\) (証明1)
\(X×(Y\cap Z) \subseteq (X×Y)\cup (X×Z)\) (証明2)
をそれぞれ証明し、両者を満たす等号=の関係を導く。
証明1
\((x, y) \in X × Y \cap Z\) とすると, \(x \in X \cap y \in (Y \cup Z)\) である。
また、\(y \in Y \cup Z\)なので、\(y \in Y \cup y \in Z\)である。
\(y \in Y\) のとき
\begin{aligned}x \in X \cap y \in Y なので、(x, y) \in X×Y \end{aligned}
\(y \in Z\)のとき
\begin{aligned}x \in X \cap y \in Z なので、(x,y) \in X × Z\end{aligned}
このうちのどちらかが成り立つので, \begin{aligned}(x, y) \in (X × Y) \cup (X × Z)\end{aligned}
前提条件より、\((x, y) \in X × Y \cap Z\)\)でもあるので、証明1は示された。
証明2
(9)式と同様に証明する。
\(Y \cap Z \subseteq Y\)、\(Y \cap Z \subseteq Y\) に直積\(X\)を組み合わせて(7)式(8)式を得る。
これを組み合わせて
\begin{aligned}X×(Y\cap Z) \subseteq (X×Y)\cup (X×Z)\end{aligned}