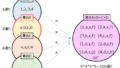
A={a,b,c},B={x,y},C={1,2,3,4},D={5,6,7}とするとき、以下の問いに答えよ。
(1)AからBへの全射写像の個数はいくつか。
(2)AからCへの単射写像の個数はいくつか。
(3)AからDへの全単射写像の個数はいくつか。
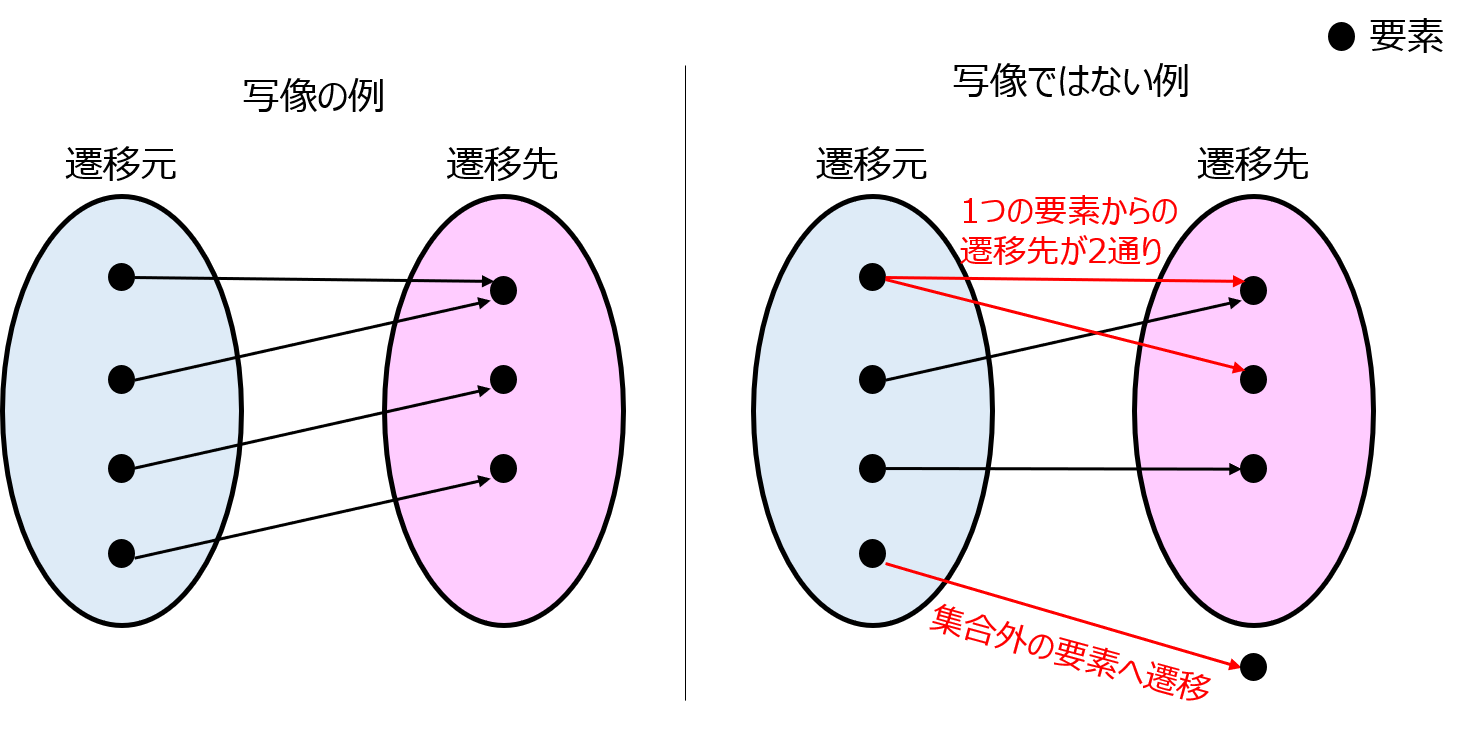
写像とは
2つの集合X、Y内にあるそれぞれの要素(x,y)の対応関係を決める規則を言います。

規則は、関数で表されることが多いです。\(f=2x\)とすると、集合X:\(X:(1,2,3,4)\)に対する写像は、\(Y:(2,4,6,8)\)のようになります。
集合\(X\)内にある各要素が集合\(Y\)にある要素に一対一で対応すること
このため、下記のような例は写像になりません。
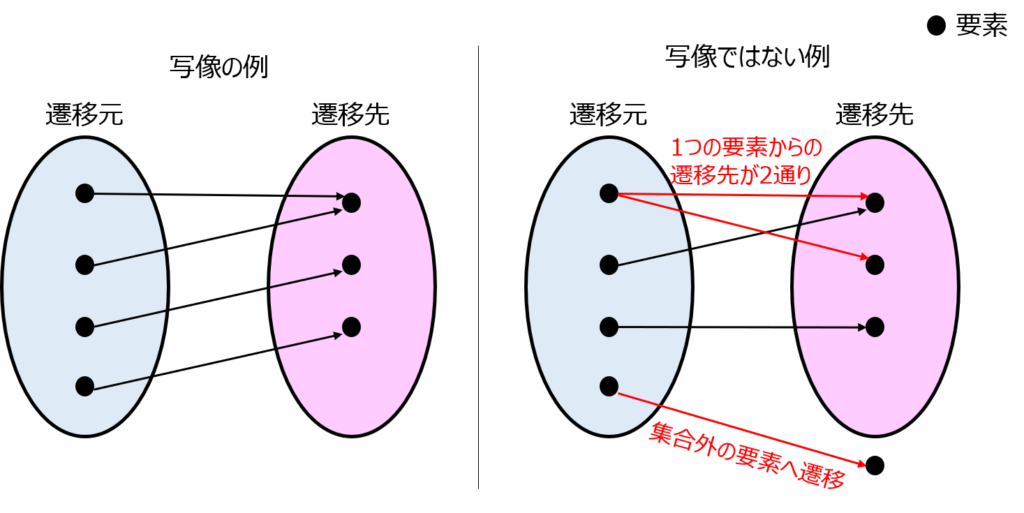
- 集合Xから集合Yへ遷移しない要素
- 集合X内の要素の遷移先が集合Yに属さない要素
- 集合X内のある要素の遷移先が集合Y内の要素複数である場合
一方で、下記の組み合わせでも写像として成立します。
- 集合Yに集合Xからの遷移先が無い要素がある
- 集合Yの各要素の遷移元に、集合X内の要素が複数存在する場合(像の衝突)
- 集合Xは空集合で、集合Yは有限集合 (関数がf=0)
全射とは
集合Xから集合Yへの写像に対し、Yの内部要素全てに遷移元の要素が存在する場合の組み合わせを言います。
数学的に述べると、下記の説明になります。
\begin{aligned}集合Yを構成する任意のyに対し、y=f(x)を満たす要素xが集合X内に存在する。\end{aligned}
- Xの要素数\(n\)がYの要素数\(m\)以上であること。\(n≧m\)

単射とは
集合Xから集合Yに対応する写像が存在し、遷移元の要素の重複が無いことを言います。
前章「写像として存在する例」2.に該当しない写像が単射になります。
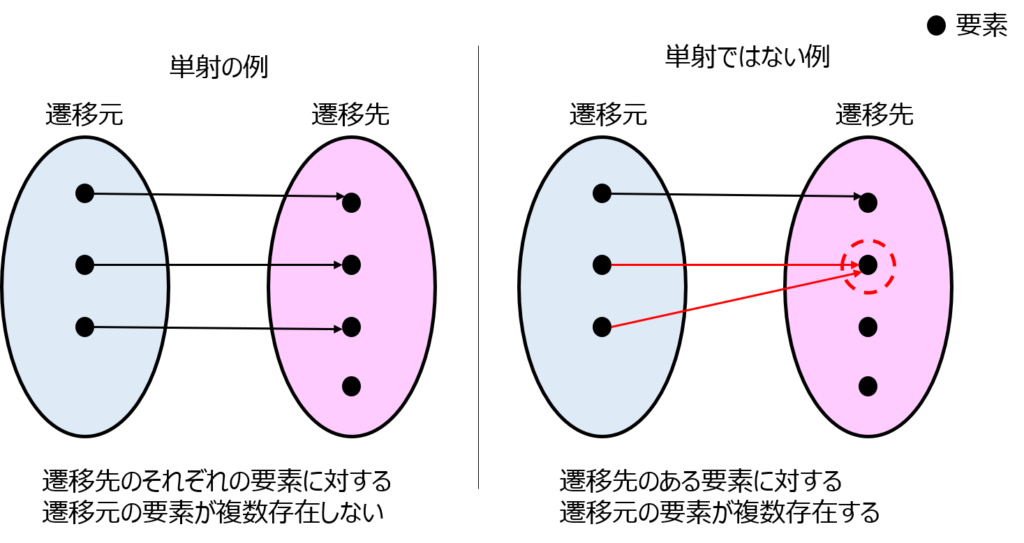
数学的には、下記の説明になります。
任意の\(x_{0},x_{1} \in X\)に対し、
\begin{aligned}x_{0}≠x_{1} ならば f(x_{0})≠f_(x_{1})\end{aligned}
- Xの要素数\(n\)がYの要素数\(m\)以下であること。\(n≦m\)
なお、下記は全て同値になります。
Aの部分集合B,C:\(B,C \subseteq A\)に対し
- \(f(B \cap C)=f(B)\cap f(C)\)
- \(f(A|B)=f(A)|f(B)\)
厳密な説明は省きますが、
遷移元の要素が2つの集合に属するならば、遷移先の要素も2つの集合に対する写像に属すること。(1.の説明)
遷移元の要素が1つの集合にしか属さない場合は、遷移先も1つの集合にのみ属すること。(2.の説明)
以上2点を意味しています。
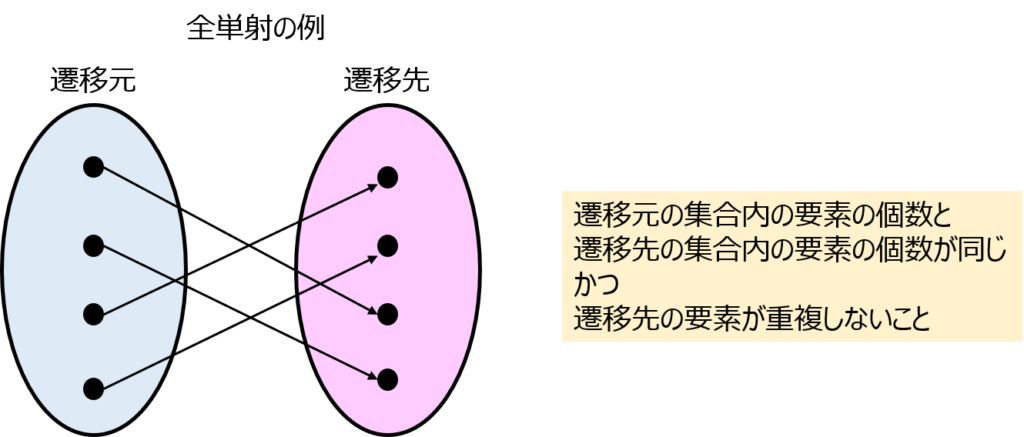
全単射とは
全射かつ単射である写像を言います。
下記のように、像の衝突は発生せず、集合Y内部の要素yそれぞれに対応する要素xも存在します。
- 集合Xと集合Yの要素数は同じ
- 集合Xの要素数がnの場合、写像の対応の個数は\(n!\)個ある。
※椅子取りゲームと同じで、1つ目の要素の遷移先はn通りあるのに対し、2つ目の要素は(n-1)通りと順次減っていくため。
合成関数における写像(全射、単射、全単射)
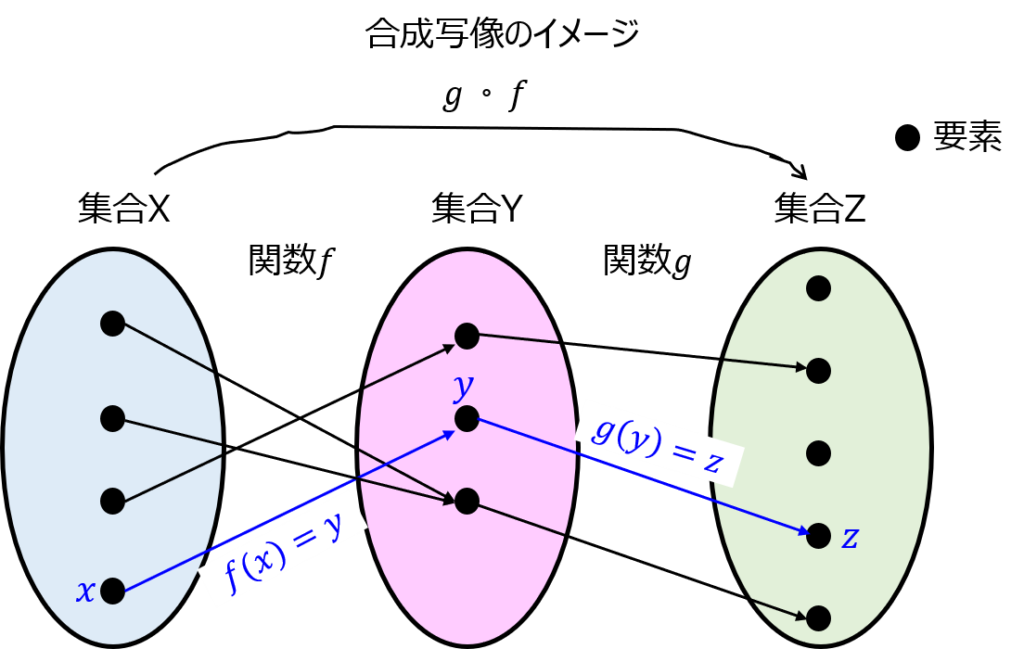
合成関数とは
合成関数とは、2つ以上の関数を写像として組み合わせ、1つの関数として見たものになります。
合成関数の記号は\(\circ\)を用います。
\begin{aligned}g \circ f=g(f(x))\end{aligned}
と表され、g(x)の引数xの部分にf(x)を丸々代入すると、合成関数になります。
合成関数の注意点
定義可能条件
\(g \circ f\)について、遷移元の集合X内の要素\(x\)に対応する像\(f(x)\)が\(g\)の定義範囲に属することです。
実数→実数を写す写像\(f(x)=x^{2}-2{x}-1\)と
自然数→実数を写す写像\(g(x)=\sqrt{x}\)の合成関数\(g \circ f\)を考える。
\(x=1\)のとき、\(f(1)=-2\)ですが、これを関数\(g\)に代入しようとすると、\(g(-2)\)のため定義範囲外です。
このように、合成写像\(g \circ f\)は定義できないことが分かりました。
合成の順番と一致性
合成関数\(g \circ f\)と\(f \circ g\)が両方定義可能であったとしても、結果が一致するとは限らないです。
\(f(x)=x^{2}+1\),\(g(x)=x+2\)の合成関数\(g \circ f\)と\(f \circ g\)を考える。
\begin{cases}g \circ f =x^{2}+1+2=x^{2}+3 \\ f \circ g=(x+2)^{2}+1=x^{2}+4x+5\end{cases}
より、両者は一致しない。
合成関数の結合即
定義可能な3つ以上の関数を合成するとき、下記の関係が成立します。
\begin{aligned}h \circ g \circ f=(h \circ g) \circ f=h \circ (g \circ f)\end{aligned}
※\(h \circ g\)、\(g \circ f\)が定義可能であることが前提です。
前節では、\(g \circ f\)、\(f \circ g\)のように合成する順番を変更すると結果が変わるとお話ししました。一方で、全体としての順番が変わらなければ、括弧()付きで合成しやすい関数から計算しても結果が変わらないことを表しています。
試験では、計算しやすい関数から順に攻めていく方針が良いと思います。
合成関数を用いた写像の性質
関数\(f,g\)について
- \(f\)と\(g\)が共に全射のとき、\(g \circ f\)も全射である
- \(f\)と\(g\)が共に単射のとき、\(g \circ f\)も単射である
- \(f\)と\(g\)が共に全単射のとき、\(g \circ f\)も全単射である
全射の証明
\(g \circ f\)の出力\(z \in Z\)を考える。
\(g\)は全射だから、ある\(y \in Y\)が存在して\(z=g(y)\)が成立する。
\(f\)も全射だから、ある\(x \in X\)が存在して\(y=f(x)\)が成立する。
二つを合わせて、
\begin{aligned}z=g(y)=g(f(x))=g \circ f(x)\end{aligned}
なる全射の写像\(g \circ f\)が存在する。
単射の証明
集合X内の異なる要素:\(x_{0},x_{1} \in X\)を考える。
\(x_{0},x_{1}\)は異なる要素のため、\(f(x_{0})≠f(x_{1})\)
\(f(x_{0})≠f(x_{1})\)のため、\(g(f(x_{0}))≠g(f(x_{1}))\)
\(g(f(x_{0}))≠g(f(x_{1}))\)なので、定義より、\(g \circ f\)は単射である。
全単射の証明
全射かつ単射であることが全単射の定義である。
よって、前節、前々節の証明を合わせると、\(f\)と\(g\)が共に全単射のとき、\(g \circ f\)も全単射であることが分かる。
解答例
(1)全射写像の個数
集合AからBへ遷移するとき、遷移先の要素が重複しても良い。ただし、Bの要素でAからの遷移元が無いパターンは除外することに注目する。
考えられる例を書き下していくと下記の6通り考えられる。
- \(f_{1}\):a→x,b→x,c→y
- \(f_{2}\):a→x,b→y,c→x
- \(f_{3}\):a→x,b→y,c→y
- \(f_{4}\):a→y,b→x,c→y
- \(f_{5}\):a→y,b→y,c→x
- \(f_{6}\):a→y,b→x,c→y
補足
集合Aの要素数をn、集合Bの要素数をm (ただし、n≧m)としたとき、全射の個数は
\begin{aligned} \sum ^{m}_{k=1}(-1)^{m-k}{}_m C_k*k^{n}\end{aligned}
個存在します。
証明は、要望が多ければ追記します。
(2)単射写像の個数
Cの要素4つの中から異なる3つを選ぶ順列のため
\begin{aligned}{}_4 P_3=4*3*2=24通り\end{aligned}
補足
上記の式でピンとくるかもしれませんが、集合Aの要素数をn、集合Bの要素数をm (ただし、n≦m)としたとき、単射の個数は
\begin{aligned}{}_n P_m個\end{aligned}
(3)全単射の個数
集合AとDの個数はお互いに同じ。重複を許さず、一対一でマッチングさせていくので
\begin{aligned}4!=4*3*2*1=24通り\end{aligned}
(鳩ノ巣原理と言います。)
最後に
本問は、電通大の院試でよく出てきます。
同大学を志望される方は、是非隅々まで理解しましょう。