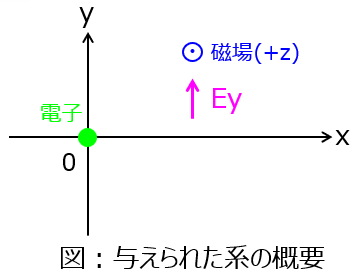
y方向の電場$E_{o}>0$、z方向の磁場$B_{o}>0$が直交している系を考える。初速度$(v_{xo},v_{yo},0)$で原点を出発した電荷$q$の荷電粒子の軌道を図示せよ。
問1 $q>0,v_{xo}=0,v_{yo}<0$
問2 $q>0,v_{xo}=0,v_{yo}=0$
問3 $q>0,v_{xo}>\frac{E_y}{B}>0,v_{yo}=0$
問4 $q<0,v_{xo}=0,v_{yo}<0$
はじめに
以前の記事では、ある特定の方向に速度を持つ荷電粒子が同じくある特定の方向にのみ成分を持つ電場、磁場で発生する運動について考察しました。
ラーモア半径の性質、ドリフト運動が発生することを学びましたが、他の向きの場合はどのような運動になるのでしょうか。同様の運動をすることが予想できますが、向きについてはイメージできていない方が私含め多いのではないかと思います。
そこで、本記事では、種々の向きを持つ電場、磁場内における荷電粒子の運動を様々な条件で見ていきます。運動方程式を解いて、その正負の関係に着目するところから始めていきますので、過去の記事をまだご覧になられていない方でも追いつける内容となっています。
解答例
前提
まず、荷電粒子にかかる運動方程式は、ローレンツ力と外力$\boldsymbol{F}$を用いて
\begin{aligned}m\dot{\boldsymbol{v}}=q\boldsymbol{v}×\boldsymbol{B}+\boldsymbol{F}\end{aligned}
これを磁場に平行な成分$\boldsymbol{F}_{\parallel}$と垂直な成分$\boldsymbol{F}_{\perp}$に分解すると,
\begin{cases}
m\boldsymbol{\dot{v}}_{\parallel} &=\boldsymbol{ F_{\parallel}} \\
m\dot{\boldsymbol{v}}_{\perp} &= q\boldsymbol{v}_{\perp}\times\boldsymbol{B} + \boldsymbol{F}_{\perp}
\end{cases}
$\boldsymbol{B}(0,0,B_0),\ \boldsymbol{E}(0,E_0,0)$ とすると
\begin{cases}
\dot{v}_x &= \pm \omega_c v_y \tag{3} \\ \dot{v}_y &= \mp \omega_c v_x + \frac{F_{\perp}}{m}
\end{cases}
ただし,複号の上側は $q>0$ の場合,下側は $q<0$ の場合を示す。上式により
\begin{cases}
\ddot{v}x &= \pm \omega_c (\mp \omega_c v_x + \frac{F_{\perp}}{m})
= -\omega_c^2 \left( v_x – \frac{F_{\perp}}{qB} \right)
\quad (B = B_0) \\
\ddot{v}_y &= -\omega_c^2 v_y
\end{cases}
式(3)より,
\begin{align}
\frac{d^2}{dt^2}\left( v_x – \frac{F_{\perp}}{qB} \right)
= -\omega_c^2 \left( v_x – \frac{F_{\perp}}{qB} \right)
\end{align}
$t=0$ で $v_x = v_{x0},\ v_y = v_{y0}$ とすれば,上式の解は
\begin{cases}
v_x &= \left( v_{x0} – \frac{F_{\perp}}{qB} \right)\cos \omega_c t
\pm v_{y0} \sin \omega_c t
+ \frac{F_{\perp}}{qB} \\
v_y &= \mp \left( v_{x0} – \frac{F_{\perp}}{qB} \right)\sin \omega_c t
+ v_{y0} \cos \omega_c t
\end{cases}
(ii) 一様直交電磁場が存在する場合,$\boldsymbol{F} = q\boldsymbol{E}$ とおいて上式を積分する。$t=0$ で $x=y=0$ とすると,
\begin{aligned}x =
\left( v_{x0} – \frac{E_y}{B} \right)
\frac{1}{\omega_c} \sin \omega_c t
\pm \frac{v_{y0}}{\omega_c}(1 – \cos \omega_c t)+\frac{E_y}{B}t
\end{aligned}
\begin{aligned}y =
\left( v_{x0} – \frac{E_y}{B} \right)
\frac{1}{\omega_c}(\pm 1 \pm \cos \omega_c t)+\frac{v_{y0}}{\omega_c}\sin \omega_c t\end{aligned}
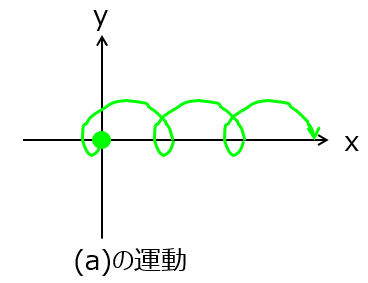
問1 $q>0,v_{xo}=0,v_{yo}<0$ のとき
\begin{cases}x = \frac{E_y}{B} \left( t – \frac{\sin \omega_c t}{\omega_c} \right)\frac{v_{y0}}{\omega_c} (1 – \cos \omega_c t) \\ y = \frac{E_y}{B} \left( \frac{1 – \cos \omega_c t}{\omega_c} \right)\frac{v_{y0}}{\omega_c} \sin \omega_c t\end{cases}
これより、下記の軌道になる。
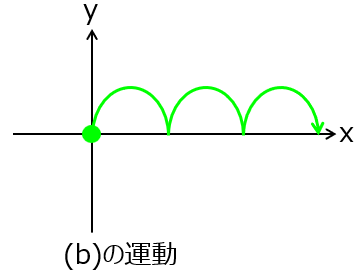
問2 $q>0,v_{xo}=0,v_{yo}=0$ のとき
\begin{cases}x = \frac{E_y}{B} \left( t – \frac{\sin \omega_c t}{\omega_c} \right) \\ y = \frac{E_y}{B} \left( \frac{1 – \cos \omega_c t}{\omega_c} \right)\end{cases}
これより、下記の軌道になる。
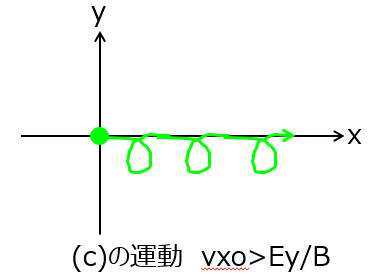
問3 $q>0,v_{xo}>\frac{E_y}{B}>0,v_{yo}=0$のとき
\begin{cases}x = \frac{E_y}{B} \left( t – \frac{\sin \omega_c t}{\omega_c} \right)\frac{v_{x0}}{\omega_c} \sin \omega_c t \\ y = \frac{E_y}{B} \left( \frac{1 – \cos \omega_c t}{\omega_c} \right)\frac{v_{x0}}{\omega_c} (1 – \cos \omega_c t)\end{cases}
これより、下記の軌道になる。
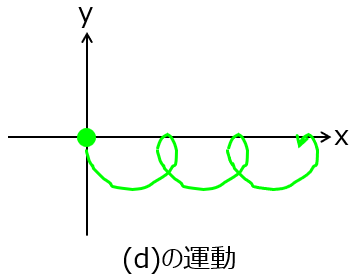
問4 $q<0,v_{xo}=0,v_{yo}<0$のとき
\begin{cases}x = \frac{E_y}{B} \left( t – \frac{\sin \omega_c t}{\omega_c} \right)
– \frac{v_{y0}}{\omega_c} (1 – \cos \omega_c t) \\ y = \frac{E_y}{B} \left( \frac{-1 + \cos \omega_c t}{\omega_c} \right)+ \frac{v_{y0}}{\omega_c} \sin \omega_c t\end{cases}
これより、下記の軌道になる。
最後に
各々の式の意味と物理現象を理解できるまで計算と変形を繰り返していきましょう。