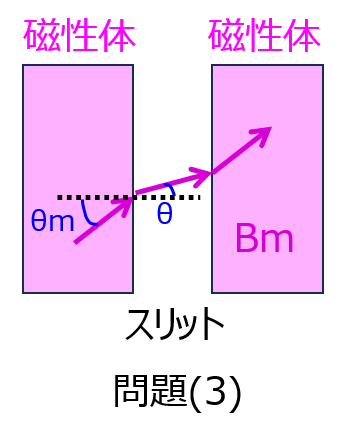
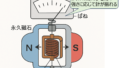
下記のように、無限に広がっている磁性体の内部に厚さdのスリットを設ける。磁性体内部の磁場が(1)~(3)それぞれの場合でかかっている時、真空領域で発生する磁場\(H\)と磁束密度\(B\)を求めよ。なお、磁性体の透磁率を\(\mu\)、真空中の透磁率を\(mu_{o}\)とする。
磁性体中の磁束密度\(\boldsymbol{B_{m}}\)が
(1)境界面に対して垂直にかかっているとき
(2)境界面に対して平行にかかっているとき
(3)境界面に対し、\(\theta_{m},\theta\)の角をなしているとき
磁性体とは
磁化ベクトルを持つ物質を言います。磁化とは、物質内部で磁気双極子モーメントが発生することを言い、これにより、物質から外部へ磁場が発生します。
現実に存在する物質は、大なり小なり磁化しますが、一般的には強く磁化される物質を磁性体と呼ぶことが多いです。
微小体積中に含まれる磁気双極子モーメントは、\(\dfrac{d\boldsymbol{m}}{dV}\)で表されます。単位体積当たりの磁気モーメントを磁化ベクトル\(\boldsymbol{M}\)で表すと、下記になります。
\begin{aligned}\boldsymbol{M}=\dfrac{d\boldsymbol{m}}{dV}\end{aligned}
このように、磁気双極子モーメントによって磁化の強さが決まります。
磁気双極子モーメントの特性
電気双極子モーメントの記事でもお話ししましたが、同様の特性を持ちます。
磁気双極子モーメント\(\boldsymbol{m}\)とし、距離r離れた位置に発生する磁場\(H\)は、磁位\(\phi_{m}\)から
\begin{aligned}\phi_{m}=\dfrac{m\cos \theta}{4 \pi r^{2}}=\dfrac{\boldsymbol{m}・\boldsymbol{r}}{4 \pi r^{2}}\end{aligned}
\(\boldsymbol{H}=-grad\phi_{m}\)だから
\begin{aligned}\boldsymbol{H}=\dfrac{1}{4 \pi} \left \lbrack \dfrac{3(\boldsymbol{m}・\boldsymbol{r})\boldsymbol{r}}{r^{5}}-\dfrac{\boldsymbol{m}}{r^{3}} \right \rbrack\end{aligned}
\begin{cases}H_{r}=\dfrac{m \cos \theta}{2 \pi r^{3}} \\ H_{\theta}=\dfrac{m \sin \theta}{ 4 \pi r^{3}}\end{cases}
になります。詳しい導出は電気双極子の記事をご覧ください。電気双極子モーメント\(\boldsymbol{p}\)を磁気双極子モーメント\(\boldsymbol{m}\)に置き換えるとできます。
解答例
電磁波の記事などで説明していますが、境界条件により解決することができます。
- 磁場\(H\):境界面の平行成分が連続
- 磁束密度\(B\):境界面の垂直成分が連続
(1)境界面に対し垂直にかかる磁場
磁束密度\(B_{m}\)が連続なので、真空中の磁束密度\(B\)も等しい。
\begin{aligned}B=B_{m}\end{aligned}
真空中の透磁率は\(\mu_{o}\)なので、真空中の磁場\(H\)は
\begin{aligned}H=\dfrac{B_{m}}{\mu_{o}}\end{aligned}
(2)境界面に対し平行にかかる磁場
磁性体中の磁場\(H_{m}=\dfrac{B_{m}}{\mu}\)が連続なので
\begin{aligned}H=\dfrac{B_{o}}{\mu}\end{aligned}
\begin{aligned}B=\mu_{o}H=\dfrac{\mu B_{o}}{\mu}\end{aligned}
(3)境界面に対し斜めに入射するとき
磁束密度\(B_{m}\)を垂直成分、接線成分に分解すると
\begin{cases}B_{m}\cos \theta_{m}=B \cos \theta \\ H_{m}\sin \theta_{m}=H \sin \theta \\ B_{m}=\mu H_{m} \\ B=\mu H \end{cases}
これを解くと、下記のように求まる。
\begin{cases}B=B_{m}\sqrt{\cos^{2} \theta +\left(\dfrac{\mu_{o}}{\mu} \right)^{2}\sin^{2} \theta} \\ H=\dfrac{B_{m}}{\mu_{o}}\sqrt{\cos^{2} \theta +\left(\dfrac{\mu_{o}}{\mu} \right)^{2}\sin^{2} \theta} \\ \theta=\tan^{-1}\left(\dfrac{\mu_{o}}{\mu}\tan \theta_{m}\right) \end{cases}
最後に
本問の類題が大阪公立大学で出題されたことがあります。電場による分極でしたが、考え方の本質ば磁場でも変わりません。