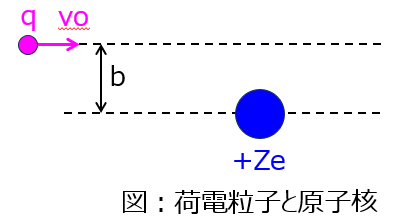
下記図のように、質量$m$、電荷$q$の荷電粒子が初速度$v_{o}$で無限遠から電荷量$Ze$の原子核へ近づいている系を考える。荷電粒子が直線で進んだ時、原子核の中心と衝突パラメータ$b$離れている場所から入射しているものとする。また、原子核の質量は非常に大きいものとする。
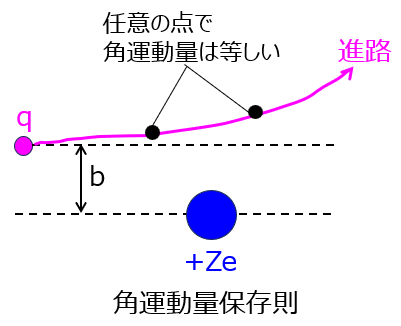
問1 荷電粒子が持つ原子核まわりの角運動量$\boldsymbol{L}$を、原子核の中心を原点とする位置ベクトル$\boldsymbol{r}$を用いて表せ。本系において、角運動量保存則が成立することを証明せよ。
問2 角運動量$\boldsymbol{L}$の大きさを求めよ。
問3 軌道上で荷電粒子が原子核に最も近づくときの粒子間の距離を$s$とする。この点における速度$v_{s}$を、$v_{o},b,s$を用いて表せ。
角運動量とは
回転運動における運動量に相当する物理量です。直線運動の運動量は、質点の質量と速度の積$\boldsymbol{p}=m\boldsymbol{v}$で表されました。角運動量の場合は、基準点からのベクトル$\boldsymbol{r}$を用いて下記で表されます。
\begin{aligned}\boldsymbol{L}&=\boldsymbol{r}×\boldsymbol{p} \\ &=m\boldsymbol{r}×\boldsymbol{v} \\ &=m \boldsymbol{r}×\boldsymbol{\dot{r}} \end{aligned}
角運動量保存則
外部からトルクが作用しない系において、角運動量は時間変化しません。これを角運動量保存則と言います。
宇宙空間による惑星運動や、本問のような粒子間にクーロン力がかかる系などで本法則は成立します。本問の類題が実際に阪大の院試(電磁理論)にて出題されたことがありました。
電気系の学生からすれば、一般教養で習ったきり忘れてしまった方もいらっしゃるかもしれません。しかし、物理を勉強していく上で基本となる概念ですので、これを機に覚え直すことを推奨します。
解答例
問1 角運動量保存則の証明
(1)式を用いて求めていく。粒子間のクーロン力は下記の式で表される。
\begin{aligned}\boldsymbol{F}=\dfrac{kqZe}{r^{2}}\dfrac{\boldsymbol{r}}{r}\end{aligned}
運動方程式により、
\begin{aligned}m\dfrac{d\boldsymbol{v}}{dt}=\dfrac{kqZe}{r^{2}}\dfrac{\boldsymbol{r}}{r}\end{aligned}
両辺に対し、ベクトル$\boldsymbol{r}$の外積を取ると
\begin{aligned}m\dfrac{d\boldsymbol{r}×\boldsymbol{v}}{dt}=\dfrac{kqZe}{r^{2}}\dfrac{\boldsymbol{r}×\boldsymbol{r}}{r}\end{aligned}
自ベクトル同士の外積は0なので、$\boldsymbol{r}×\boldsymbol{r}=0$
上式の右辺は0であるため、左辺も0。
\begin{aligned}m\boldsymbol{r}×\boldsymbol{v}=\boldsymbol{L}=0\end{aligned}
が成立し、角運動量保存則を表す。
問2 角運動量の計算
問1により、角運動量保存則が成立するので、任意の時間において$\boldsymbol{L}$は一定である。t=0のときの角運動量を求められれば一般性も損なわれないため
\begin{aligned}L=mv_{o}b\end{aligned}
問3 最接近地点における$s$
角運動量保存則により、t=0の地点と最接近点における角運動量は等しい。
\begin{aligned}mv_{o}b=mv_{s}s\end{aligned}
\begin{aligned}v_{s}=\dfrac{v_{o}b}{s}\end{aligned}
補足
本問では、原子核の電荷量が正だったので、荷電粒子には斥力が働きます。$b$の大きさにもよりますが、下記のような進路を取ることがイメージできます。
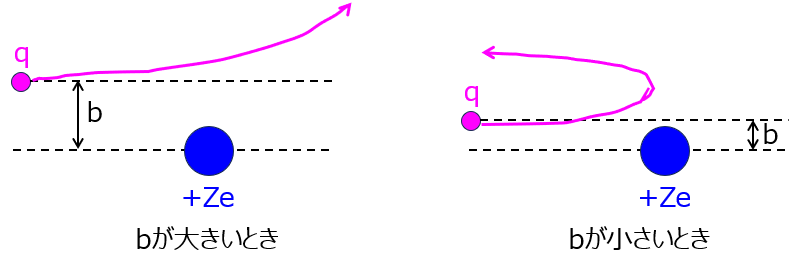
※$b$が小さければ斥力が強く、原子核に届く前に追い返されます。一方で、十分に離れている時は、軌道がずれるものの、原子核を通り過ぎること考えられます。
一方で、負の場合は引力が働くので下記のような軌道になります。
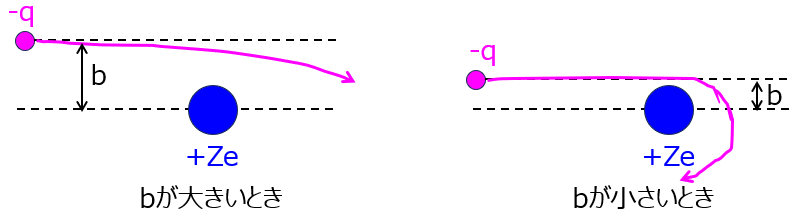
荷電粒子の運動について、図示することを求める問題はちらほら出てきます。合わせて理解しておきましょう。