数学 複素積分を利用したフレネル積分の求値問題
この記事で覚えてほしいこと\(√x=z\)と置き、積分対象の関数を三角関数型\(\cos(x^{2})\)に変換する。\(exp(-iz^{2})\)型の積分を与えられた閉路\( C_{1} , C_{2} , C_{3}\)を用いて行う。積分結果の実部が与えられた結果にあたる。
数学 
数学 留数定理を利用した有理関数の複素積分と逆ラプラス変換
留数定理とは正則関数が閉曲線$C$の内部で有限個の孤立特異点$a_{1},a_{2},\cdots,a_{n}$を持つとき、下記の関係が成り立つことを言います。\begin{aligned}\int_{c}f(z)dz=2 \pi i \sum^{n}_{k=1}\mathrm{Res}(f,a_k)\end{aligned}
機械 振動系の周波数を変化させたときの振幅の応答と共鳴曲線
共鳴曲線とは外力の振動数を変化させたときの定常応答振幅の変化を表す曲線を言います。制御工学でも用いられることはありますが、古典力学の範囲でも解くことが出来ます。
機械 気体分子運動論によるポアソンの式の導出問題
問題下記のように、長さ LL の立方体の容器に，単原子理想気体が閉じこめられている。立方体の壁に分子が弾性衝突したとき、衝突方向に向かって壁が動き、体積も変わる前提で下記の問1~4に答えよ。問1：分子の衝突x=Lx=L の壁が気体分子の x...
コラム 院試ではホワイト研究室の志望をオススメする理由3選
身も蓋も無いですが、リスクヘッジです。残念なことに、研究室が合わずに中退してしまう方が毎年一定数存在します。勿論、本人の資質にもよる部分はあるかもしれません。ただ、その方々は、共通してブラック研究室所属であることが多いです。
コラム 会社でよく使うため、履修をオススメする大学の講義
統計学これは疑いようが無いです。電気系、情報系に限らず、技術系の職種で必ず使うと断言できます。なぜならば、実験、技術検討する上で必ずデータを相手にするからです。データの素性、平均、分散、最大値など、読み取れる結果から結論づける際の根拠として必ず使用します。
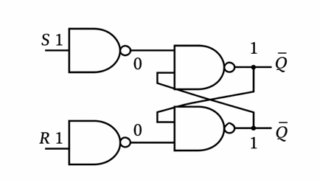
情報 SRフリップフロップの動作内容と論理回路の作成問題
SRフリップフロップとは二入力(S：セット、R：リセット)を用いて、出力0,1を切り替える順序回路になります。一度S=1を入力すると、リセットR=1を入力するまで出力1を立て続けます。(ラッチ)なお、S=1とR=1を同時に入力することは禁止です。
電気回路 【例題付き】合成インピーダンス、アドミタンスの公式と最適な使い方
インピーダンス、アドミタンスの合成式の使い分け回路の並列数で考える。直列に合成する要素があり、並列回路数が2つまで：合成インピーダンスを使用(回路1)それ以外：合成アドミタンス(回路2)
情報 相手に伝わるタイムチャートの書き方を例題形式で解説
タイムチャートの書き方信号が変化するタイミングで縦線を引き、同じ時間で変化している他の信号を明確にする。波形と波形の間に矢印を追記し、信号の入出力関係を明確にする定義元の信号は上に、参照側の信号は紙面下に書く複数の信号である小機能を実現している際は、グループ化する
電気回路 高校と大学の電気回路の違いと勉強方針、初学者向けのオススメ参考書
大学における電気回路学計算に複素数、行列、微分方程式が入るようになった。ことに尽きます。オームの法則、キルヒホッフの法則の使用を基本として回路方程式を立てることに変わりませんが、数学的な計算が難しくなります。