下記のブリッジ回路の平衡条件を求めよ。
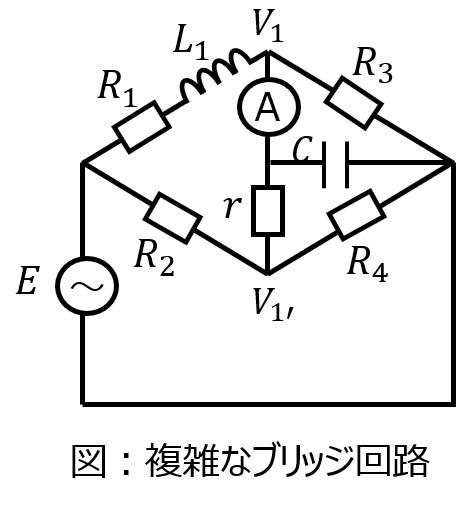
π-T変換とは
π型回路とT型回路の変換則を言います。
π型回路のインピーダンスを\(Z_{12},Z_{31},Z_{23}\)、T型回路のインピーダンスを\(Z_{1},Z_{2},Z_{3}\)と置くと下記の関係式で表されます。
\begin{cases}Z_{1}=\dfrac{Z_{12}Z_{31}}{Z_{12}+Z_{23}+Z_{31}} \\ Z_{2}=\dfrac{Z_{23}Z_{12}}{Z_{12}+Z_{23}+Z_{31}} \\ Z_{3}=\dfrac{Z_{31}Z_{23}}{Z_{12}+Z_{23}+Z_{31}}\end{cases}
どの式も分母は共通です。分子に何の文字を置くのか暗記が難しいですが、筆者の暗記方法を下記に示します。
インピーダンス\(Z_{1}\)は左に位置するが、分子に持ってくるインピーダンスは、左に位置しない\(Z_{12},Z_{31}\)。同様に、\(Z_{2}\)は中央、\(Z_{3}\)は右に位置しないインピーダンスを持ってくると、上記の等式が成立する。
このように、回路の位置する場所に該当しない素子を分子に持ってくるとうまく行きます。
なお、\(Z_{1}=1/Y_{1}\)で、他のインピーダンスに対しても同じであることから、アドミタンスに置き換えた場合、下記の等式が成立します。
\begin{cases}Y_{12}=\dfrac{Y_{1}Y_{2}}{Y_{1}+Y_{2}+Y_{3}} \\ Y_{23}=\dfrac{Y_{2}Y_{3}}{Y_{1}+Y_{2}+Y_{3}} \\ Y_{12}=\dfrac{Y_{3}Y_{1}}{Y_{1}+Y_{2}+Y_{3}} \end{cases}
関係式の導出
色々な方法がありますが、F行列の考え方を用いるのが最も楽だと考えます。(単純な行列計算と係数比較で済むので)
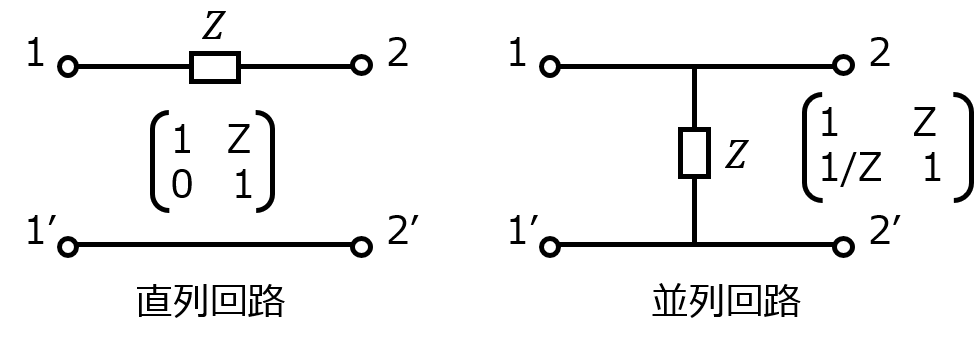
端子1-2の間にインピーダンスを直列で接続する場合、並列で接続する場合それぞれのF行列\(F_{1},F_{2}\)は
\begin{cases}F_{1}=\begin{pmatrix} 1 & Z \\ 0 & 1 \end{pmatrix} \\ F_{2}=\begin{pmatrix} 1 & 0 \\ 1/Z & 1 \end{pmatrix}\end{cases}
であるから、π型回路のF行列\(F_{\pi}\)、T型回路のF行列\(F_{T}\)は
\begin{aligned}F_{\pi}&=F_{2}F_{1}F_{2} \\ &=\begin{pmatrix} 1+\dfrac{Z_{12}}{Z_{23}} & Z_{12} \\ \dfrac{Z_{12}+Z_{12}+Z_{23}}{Z_{13}Z_{23}} & 1+\dfrac{Z_{12}}{Z_{13}} \end{pmatrix}\end{aligned}
\begin{aligned}F_{T}&=F_{1}F_{2}F_{1} \\ &=\begin{pmatrix} 1+\dfrac{Z_{1}}{Z_{3}} & \dfrac{Z_{1}Z_{3}+Z_{2}Z_{3}+Z_{1}Z_{2}}{Z_{3}} \\ \dfrac{1}{Z_{3}} & 1+\dfrac{Z_{2}}{Z_{3}} \end{pmatrix}\end{aligned}
それぞれの行列の成分を比較する。
(2,1)成分により、
\begin{aligned}Z_{3}=\dfrac{Z_{13}Z_{23}}{Z_{31}+Z_{12}+Z_{23}}\end{aligned}
(1,1)成分により、
\begin{aligned}Z_{1}&=\dfrac{Z_{12}}{Z_{23}}Z_{3} \\ &=\dfrac{Z_{12}Z_{31}}{Z_{12}+Z_{23}+Z_{31}}\end{aligned}
(2,2)成分により、
\begin{aligned}Z_{2}&=\dfrac{Z_{12}}{Z_{13}}Z_{3} \\ &=\dfrac{Z_{23}Z_{12}}{Z_{12}+Z_{23}+Z_{31}}\end{aligned}
電力工学におけるΔ-Y変換
π-T変換は、電力関係の科目だとΔ-Y変換と呼ばれることがあります。(内容は同じです。)
これは、三相交流の計算でよく使われ、表記方法がΔとYに似ているからです。
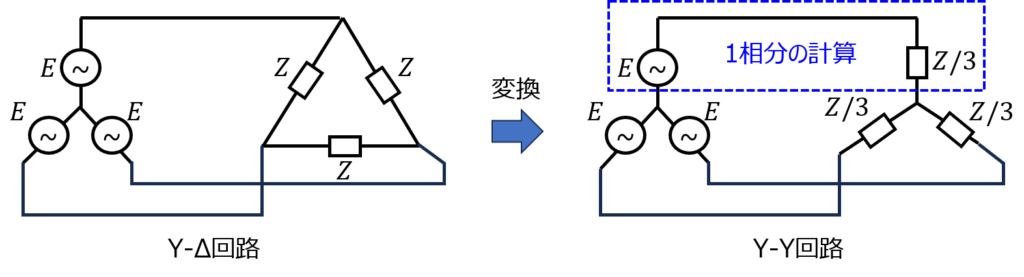
使い方として、下記のような三相交流回路を考えます。左側の電源がY型で、右側の負荷がΔ型です。このままでは計算しづらいです。しかし、Δ-Y変換(π-T変換)を用いることで、右側の回路も左側と同じY型になるため、一相分の計算に帰着することができます。
他、Δ-Y変換の特性として、位相特性がよく問われます。
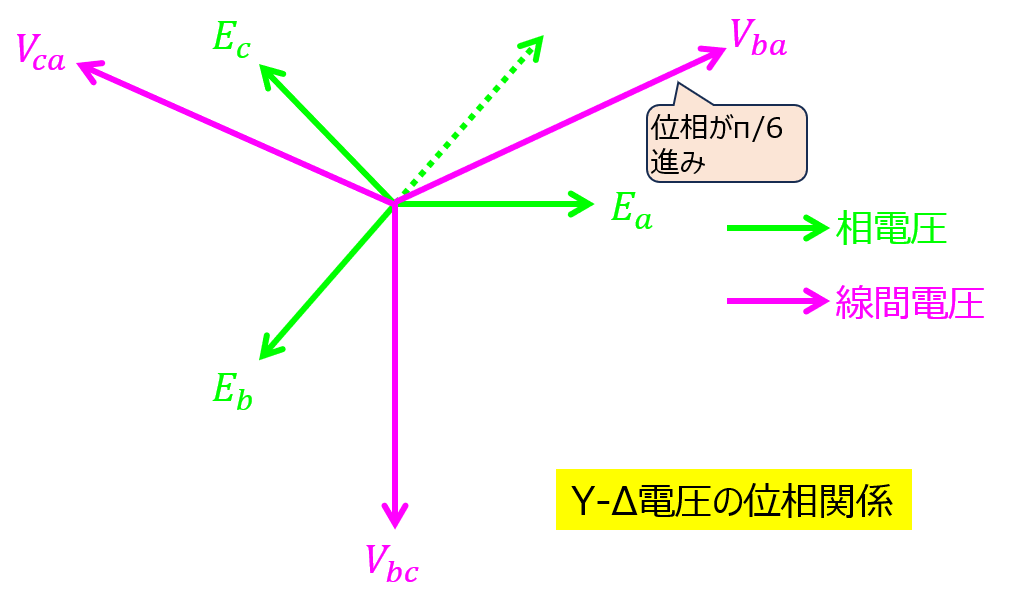
相電圧を基準に取ると、線間電圧は下記の関係になります。
相電圧は、線間電圧に対し
- π/6位相が遅れている
- 大きさは1/√3である
1.2.はベクトル図を合成すると、導くことができます。(下記)
三相目のベクトルを反転させるところがキーです。ここだけ覚えておきましょう。
また、電験3種の頻出問題になります。是非得点しましょう。
解答例
(1)平衡条件
π-T変換を用いて、ブリッジ回路の三角部分をT型に変換する。

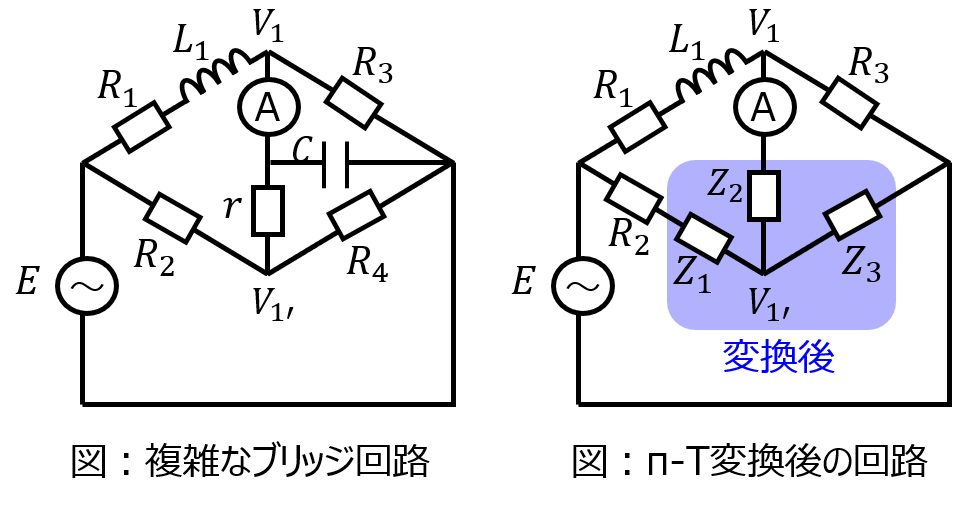
\begin{cases}Z_{1}=\dfrac{rR_{4}}{r+R_{4}+\dfrac{1}{j \omega C}}=\dfrac{j \omega CrR_{4}}{1+j \omega C(r+R_{4})} \\ Z_{2}=\dfrac{\dfrac{r}{j \omega C}}{r+R_{4}+\dfrac{1}{j \omega C}}=\dfrac{r}{1+j \omega C(r+R_{4})} \\ Z_{3}=\dfrac{\dfrac{R_{4}}{j \omega C}}{r+R_{4}+\dfrac{1}{j \omega C}}=\dfrac{R_{4}}{1+j \omega C(r+R_{4})} \end{cases}
これを用いると、ブリッジ回路の平衡条件は
\begin{aligned}(R_{1}+j \omega L)Z_{3}=(R_{2}+Z_{1}R_{3}) \end{aligned} \begin{aligned}R_{1}R_{4}-R_{2}R_{3}+j \omega{LR_{4}-C(rR_{2}R_{3}+R_{2}R_{3}R_{4}+rR_{3}R_{4})}=0 \end{aligned}
実部=虚部=0を考えて
\begin{cases}R_{1}R_{4}=R_{2}R_{3} \\ \dfrac{L}{C}=\dfrac{R_{3}}{R_{4}}(rR_{2}+R_{2}R_{4}+rR_{4})\end{cases}