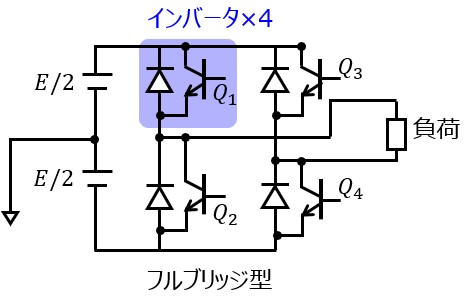
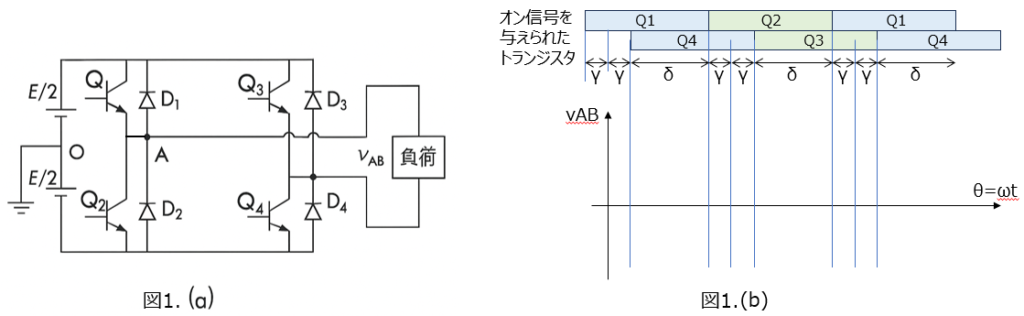
図1(a)に単相インバータの回路を示す。ここで、Q1 ~ Q4 はトランジスタを、D1 ~ D4 はダイオードを示し、理想的なスイッチング動作を行うものとする。また、これらの素子のオン電圧降下は無視する。電圧 E を出力する直流電源は二分割され、中点は接地されている。回路動作はすべて周期定常状態にあるものとし、以下の問いに答えよ。
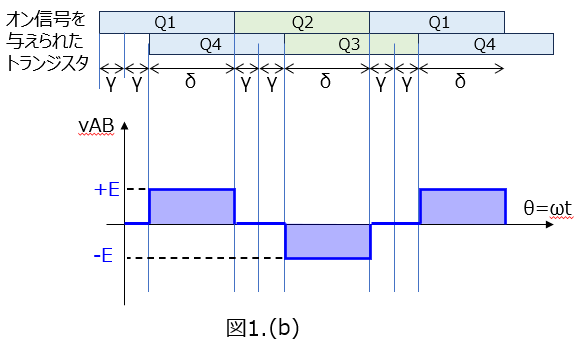
(i) 図1(b)に示すように各トランジスタにオン信号を与えた。AB間に発生する電圧 vAB の波形を描け。ただし、図1(b)と同様の図を描き、そこに波形を記入すること。ここで、t は時刻、ω は出力電圧の角周波数、θ は ωt で表される位相をそれぞれ表すものとする。また、γ、δ は図中に示される角度である。
(ii) 図1(b)で求めた vAB の基本波成分の実効値 V1 を電圧 E、角度 δ を用いて表わせ。
(iii) 図1(b)で求めた vAB の実効値 VRMS を電圧 E、角度 δ を用いて表わせ。
(iv) 図1(b)で求めた vAB の波形の総合ひずみ率(Total Harmonic Distortion: THD)を角度 δ を用いて表わせ。
(v) 負荷が誘導性であるときに、ダイオード D1 ~ D4 の役割を説明せよ。
単相インバータ回路とは
インバータにより回路の導通状態を切り替え、直流入力電圧の正負の向きを切り替える回路を言います。
ハーフブリッジ型、フルブリッジ型2種類あり、本問ではフルブリッジ型を扱っています。
それぞれ、下記の特徴があります。
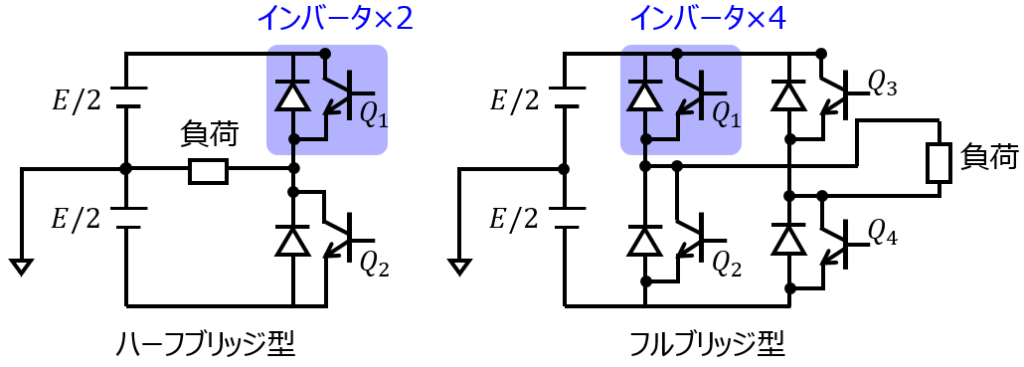
| 項目 | ハーフブリッジ | フルブリッジ |
| インバータ | 2個 | 4個 |
| 出力電圧 | ±Vdc/2 | ±Vdc,0 |
| 電圧利用効率 | 低い | 高い |
| 回路 | 簡単 | やや複雑 |
| 用途 | 小容量、学習用 簡易インバータ | モータ駆動、UPS 太陽光発電の交直変換 |
フルブリッジ型の場合、使用するインバータの数は多くなりますが、切り替えられる出力電圧のレベルが大きくなります。下記で見ていきましょう。
動作概要
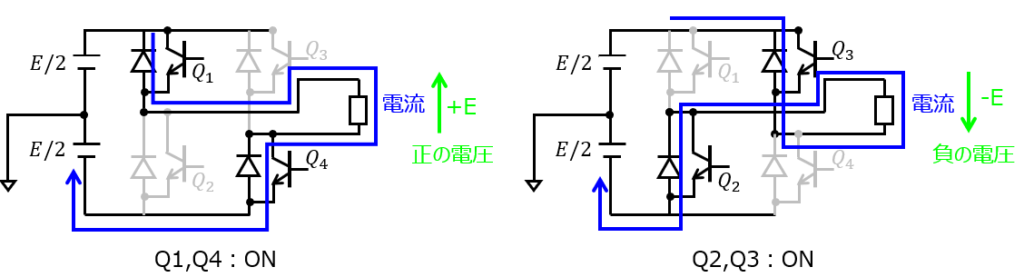
フルブリッジ型の概要を説明します。動作モードとして、インバータを2つずつONにする場合が存在します。4つのインバータを2つずつONする組み合わせは、全体4C2=4*3/2=6通りありますが、$Q_{1},Q_{2}$および$Q_{3},Q_{4}$をの場合、電源に対し直で短絡になります。よって、この場合を除いた4通りを考えます。
- $Q_{1},Q_{4}$をONにしたとき:
電源電圧に対し順方向に電流が流れるため、正の電圧+Eが出力されます。 - $Q_{2},Q_{3}$をONにしたとき:
電源電圧に対し逆方向に電流が流れるため、負の電圧-Eが出力されます。 - $Q_{1},Q_{3}$または$Q_{2},Q_{4}$ををONにしたとき:
還流部分にしか電流は流れず、電圧源も存在しないため、電圧0が出力されます。
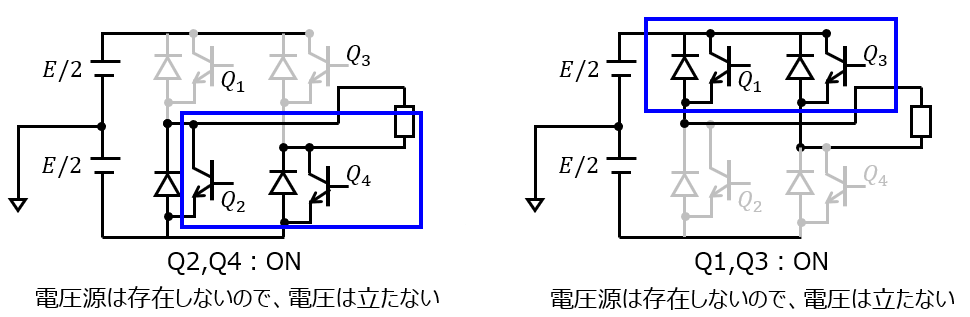
このように、三つのレベルの出力電圧を出力可能な3レベルインバータとしてふるまいます。
ハーフブリッジ型の場合、電圧源無しで還流可能な区間は取れないため、出力は±Eの2通りを取ります。
総合ひずみ率
出力波形のひずみの程度を表す量で、基本波に対する高調波の比になります。
\begin{aligned}THD=\dfrac{全高調波の実効値}{基本波の実効値}\end{aligned}
(4)を解くうえで用います。(1)~(3)は誘導です。
解答例
(1)出力波形の図示
前節の動作概要で説明した通り、各インバータがONになっている時刻それぞれに対し回路を考えて出力電圧を書けば良いです。
(2)基本波成分の実効値
$v_{AB}$は奇関数であるため、偶数次の成分は0になる。$n=1,3,5 \cdots$を考えて
\begin{aligned}v_{AB}(\theta)=\sum^{\infty}_{n=1,3,5 \cdots} b_{n} \sin (n \theta)\end{aligned}
\begin{aligned}b_{n}=\dfrac{2}{\pi}\int^{\pi}_{0}v_{AB}(\theta) \sin(n \theta) d\theta\end{aligned}
$v_{AB}$は$\gamma<\theta<\pi-\gamma$で+Eになる。
\begin{aligned}b_{n}&=\dfrac{2}{\pi} \int^{\pi-\gamma}_{\gamma}E \sin(n \theta)d \theta \\ &=\dfrac{2E}{\pi} \left \lbrack -\dfrac{\cos(n \theta)}{n} \right \rbrack^{\pi-\gamma}_{\gamma} \\ &=\dfrac{2E}{n\pi}(\cos n(\pi-\gamma)-\cos(n \gamma)) \\ &=\dfrac{4E}{\pi}\cos \gamma \end{aligned}
$2 \gamma+\delta=\pi$より、$\gamma=\frac{\pi-\delta}{2}$
基本波成分(n=1)の振幅$b_{1}$は
\begin{aligned}b_{1}&=\dfrac{4E}{\pi} \cos \left(\dfrac{\pi-\delta}{2}\right) \\ &=\dfrac{4E}{\pi}\sin \delta\end{aligned}
実効値は、上式を1/√2倍すれば良いので、$V_{1}=\dfrac{2 \sqrt{2}E}{\pi}\sin(\delta/2)$
(3)$v_{AB}$の実効値$V_{RMS}$
$v_{AB}$の二乗平方根を取れば良い。π~2πの領域において、出力波形の対称性を考慮し
\begin{aligned}v_{RMS}&=\sqrt{\dfrac{1}{2 \pi}\int^{2\pi}_{0}v_{AB}(\theta)^{2}d \theta } \\ &=\sqrt{\dfrac{1}{\pi}\int^{\pi-\gamma}_{\gamma}v_{AB}(\theta)^{2}d \theta }\\ &=\sqrt{\dfrac{1}{ \pi}\int^{\pi-\gamma}_{\gamma}E^{2}d \theta } \\ &=\sqrt{\dfrac{1}{ \pi} E^{2}(\pi-2 \gamma)} \\ &=E\sqrt{\dfrac{\delta}{\pi}}\end{aligned}
なお、(2)で導いた$\gamma=\frac{\pi-\delta}{2}$を用いました。
(4)総合ひずみ率
\begin{aligned}THD&=\dfrac{\sqrt{\dfrac{E^{2}\delta}{\pi}-\dfrac{8E^{2}}{\pi^{2}} \sin^{2} \frac{\delta}{2}}}{\dfrac{2 \sqrt{2}E}{\pi}\sin^{2}\frac{\delta}{2}} \\ &=\dfrac{\sqrt{\delta \pi-8\sin^{2}\frac{\delta}{2}}}{2 \sqrt{2}\sin^{2}\frac{\delta}{2}}\end{aligned}
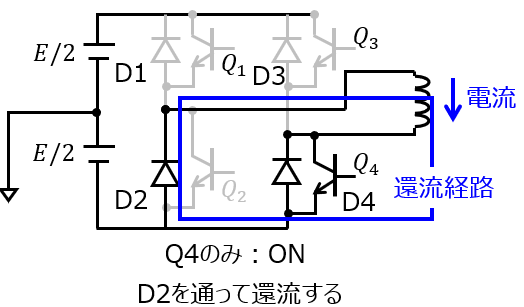
(4)ダイオード$D_{i}$の役割
ダイオードD1~D4は、トランジスタがオフになった際に発生する誘導性負荷からの逆起電力による過電圧から回路を保護する役割を果たします。
負荷が誘導性である場合、インダクタンスに蓄えられたエネルギーを放出する必要があります。ダイオード D1 から D4 は、このエネルギーの還流(回生)経路を持ちます。例えば、Q1 と Q4 がオンになっていた状態で、Q1 がオフになると、電流はダイオード D2 と D4 を通って還流します。 このような原理で回路の保護に寄与します。
最後に
本問は、パワーエレクトロニクス科目に分類されますが、この一記事のために一つのカテゴリーを作成するのは気が引けました。無論、電子回路の科目として院試で出題されることはまずないと思います。暫定的に電子回路の分類とし、パワエレに関する記事も増えた時は正式に分けるかもしれません。