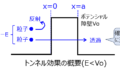
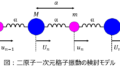
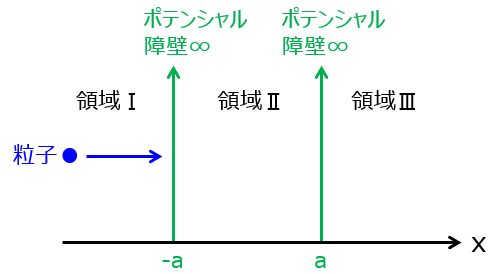
$x=±a$でデルタ関数型の障壁を持つ系における粒子の分布を考える。シュレーディンガー方程式は下記で表される。
\begin{aligned}\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi(x) -2aV_{o}\delta(x^{2}-a^{2})\psi(x) = E \psi(x)\end{aligned}
なお、$a,V_{o}$は正の定数である。
問1:(1式)を解き、波動関数の分布を偶関数、奇関数ともに求めよ。
問2:$a$を変化させたときのエネルギー固有値の変化について考察せよ。
はじめに
過去の記事では、井戸型ポテンシャル、トンネル型ポテンシャルの場合の粒子の振る舞いについて解説してきました。一方で、院試ではデルタ型ポテンシャルの場合も問われます。過去2記事に対し補充する位置づけで本問も紹介します。
微分方程式を数式的に解き、出て来た結果に対して物理現象を考察する基本作業は変わりませんが、二乗のδ関数の性質について詳しく知っておく必要があります。
デルタ関数の性質
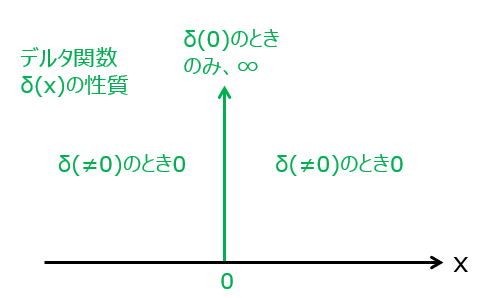
関数の引数が0になるとき、$\delta(0)=\infty$、それ以外のときは0になる関数です。インパルス関数とも呼ばれたりします。
本問では、以下の性質を用います。
\begin{aligned}\delta(f(x))=\sum \dfrac{1}{|f'(x=a_{i})|}\delta(x-a_{i})\end{aligned}
問いで与えられたデルタ関数の場合、下記の関係になります。
\begin{aligned}\delta(x^{2}-a^{2})=\dfrac{\delta(x+a)-\delta(x-a)}{2a}\end{aligned}
この関係を用いて問題を解いていきます。
解答例
問1:波動関数の分布
(3式)を(1式)に代入して
\begin{aligned}\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi(x) -V_{o}(\delta(x+a)-\delta(x-a))\psi(x) = E \psi(x)\end{aligned}
$x<-a,-a<x<a,a<x$、3つの領域における波動関数を求める。
(i)x<-aのとき
\begin{aligned}\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi(x) = E \psi(x)\end{aligned}
\begin{aligned}\frac{d^2}{dx^2} \psi(x)=-\dfrac{2mE}{\hbar^{2}}\psi(x)\end{aligned}
\(x →-\infty \)としたとき、\(\psi(x)→0\)のため、\(e^{- \alpha x}\)成分は存在せず、\(e^{\alpha x}\)のみ考える。求める波動関数は
\begin{cases}\psi_{I}(x)=Ae^{\alpha x} \\ \alpha=i\sqrt{\frac{2mE}{\hbar^{2}}}\end{cases}
ただし、$A$は定数である。
(iii)a<xのとき
同じ議論で$B$を定数とし
\begin{aligned}\psi_{III}(x)=Be^{-\alpha x}\end{aligned}
(ii)-a<x<aのとき
ポテンシャル障壁に囲まれているため、\(e^{- \alpha x}\)、\(e^{ \alpha x}\)2つの重ね合わせを考慮し
\begin{aligned}\psi_{II}(x)=Ce^{\alpha x}+De^{-\alpha x}\end{aligned}
次に、境界条件により具体的な波動関数の分布を求める。
$x=-a,a$それぞれの地点において、(7式)と(9式)、(8式)と(9式)が連続である。
$\psi_{I}(-a)=\psi_{II}(-a),\psi’_{I}(-a)=\psi’_{II}(-a)$および
$\psi_{III}(-a)=\psi_{II}(-a),\psi’_{III}(-a)=\psi’_{II}(-a)$なので
\begin{cases}Ae^{\alpha a}=Ce^{\alpha a}+De^{-\alpha a} \\ (\alpha Ce^{-\alpha a}- \alpha De^{\alpha a})-\alpha Ae^{-\alpha a}=\dfrac{2mV_{o}}{\hbar^{2}}A^{-\alpha a} \\ Be^{-\alpha a}=Ce^{\alpha a}+De^{-\alpha a} \\ -(\alpha Ce^{\alpha a}- \alpha De^{-\alpha a})-\alpha Be^{-\alpha a}=\dfrac{2mV_{o}}{\hbar^{2}}B^{-\alpha a}\end{cases}
ただし、(10式)の第二式は、(4式)を区間[-a-ε,-a+ε]で積分し
\begin{aligned}-\dfrac{\hbar^{2}}{2m}\left( \dfrac{d \psi(x)}{dx}|_{x=-a+\varepsilon}-\dfrac{d \psi(x)}{dx}|_{x=-a-\varepsilon} \right)-V_{o}\psi(-a)=E\int^{-a+\varepsilon}_{-a-\varepsilon}\psi(x) dx\end{aligned}
$\varepsilon→0$の極限を考えると、無限ポテンシャルにあたり、内部の波動関数は0(=右辺0)になるので
\begin{aligned}\mathop{\mathrm{lim}}\limits_{\varepsilon→0}\psi'(-a+\varepsilon)-\mathop{\mathrm{lim}}\limits_{\varepsilon→0}\psi'(-a-\varepsilon)=-\dfrac{2m}{\hbar^{2}}V_{o}\psi(-a)\end{aligned}
であることを用いました。(10式)の第四式も$x=a$で同様の計算をすると得られます。
(10式)の上2つ、下2つをそれぞれ連立することで
\begin{aligned}Ce^{-\alpha a}=\left(\dfrac{\alpha \hbar^{2}}{mV_{o}}-1 \right)D e^{\alpha a} \\ De^{-\alpha a}=\left(\dfrac{\alpha \hbar^{2}}{mV_{o}}-1 \right)C e^{\alpha a}\end{aligned}
対称式となるので、上式が両方成立するためには、$D=±C$
(10式)の第一式、第三式にそれぞれ代入する。
$D=C$のときは、偶関数型の解となり
\begin{aligned}A=B=2C e^{\alpha a}\cosh \alpha a\end{aligned}
\begin{aligned}\psi(x)=\begin{cases}2C e^{\alpha (x+a)} \cosh \alpha a \\ 2C\cosh \alpha a \\ 2C e^{\alpha (-x+a)} \cosh \alpha a\end{cases}\end{aligned}
$D=-C$のときは、奇関数型の解となり
\begin{aligned}A=B=2C e^{\alpha a}\sinh \alpha a\end{aligned}
\begin{aligned}\psi(x)=\begin{cases}2C e^{\alpha (x+a)} \sinh \alpha a \\ 2C\sinh \alpha a \\ 2C e^{\alpha (-x+a)} \sinh \alpha a\end{cases}\end{aligned}
問2:エネルギー固有値の振る舞い
まず、偶関数に対して考える。
$\alpha$を決定し、(7式)の第2式に代入すれば良い。準備として(13式)に$D=C$を代入すると
\begin{aligned}1+e^{-2 \alpha a}=\dfrac{\hbar^{2}}{mV_{o}}\alpha\end{aligned}
$a$を0,∞に近づけた時の$\alpha$の極限を考える。
\begin{aligned}\alpha=\begin{cases}\dfrac{2mV_{o}}{\hbar^{2}} \quad (a→0) \\ \dfrac{mV_{o}}{\hbar^{2}} \quad (a→\infty)\end{cases}\end{aligned}
これを(7式)に代入して$E$について整理すると、$E$の固有値は
\begin{aligned}E=\begin{cases}-\dfrac{2mV_{o}^{2}}{\hbar^{2}} \quad (a→0) \\ -\dfrac{mV_{o}^{2}}{\hbar^{2}} \quad (a→\infty) \end{cases}\end{aligned}
aが大きくなるほど、エネルギー固有値は増加することが分かる。
次に、奇関数の場合を考える。
(13式)に$D=-C$を代入すると
\begin{aligned}1-e^{-2 \alpha a}=\dfrac{\hbar^{2}}{mV_{o}}\alpha\end{aligned}
同じく、$a$を0,∞に近づけた時の$\alpha$の極限を考える。
\begin{aligned}\alpha=\begin{cases}0 \quad (a→0) \\ \dfrac{mV_{o}}{\hbar^{2}} \quad (a→\infty)\end{cases}\end{aligned}
同じく、これを(7式)の第二式に代入して$E$の固有値を考える。
\begin{aligned}E=\begin{cases}0 \quad (a→0) \\ -\dfrac{mV_{o}^{2}}{2\hbar^{2}} \quad (a→\infty) \end{cases}\end{aligned}
aを大きくすると、固有値は減少することが分かる。
最後に
誘導によっては、δ関数の下記の性質を用いてシュレーディンガー方程式を求められる場合があります。
\begin{aligned}\int^{\infty}_{-\infty}f(x) \delta(x-a)dx=f(a)\end{aligned}
デルタ関数付きの関数$f(x)$を積分した時、結果はδ関数が非零になる$x=a$の時の値$f(a)$になります。これも良く出てくるので覚えておきましょう。