ジョルダン標準形を用いた行列の準対角化

下記の行列Aをジョルダン標準形を用いて対角化せよ。その後、\(A^{n}\)を求めよ。

\begin{eqnarray}A=\begin{pmatrix} 1 & 1 \\ -1 & 3 \end{pmatrix}\end{eqnarray}
東北大学電気情報系院試 2009年8月大問(2)より引用

はじめに
本問で覚えたいこと
解答例
最後に
参考文献

はじめに

行列の対角化は、多数の大学の院試で頻出問題になっています。1問しか演習できないが、おすすめの行列の問題を紹介して欲しいと言われたら、対角化の問題を紹介するレベルです。

このように、非常に重要度の高い分野ですが、本問は一癖あります。

固有値を求め、それに対応する固有ベクトルを算出する。求めた固有ベクトルを用いて行列を作成し、これを用いて対角化。

が、一般的な流れですが、本問では、固有値が1つ(重解)で、固有ベクトルが1つしか作れません。

このままでは対角化できないですが、ジョルダン標準形を用いると解決します。

厳密には対角行列ではありませんが、行列\(A\)を\(A^{n}\)まで求められる形に何とか変形することができます。

本問で覚えたいこと

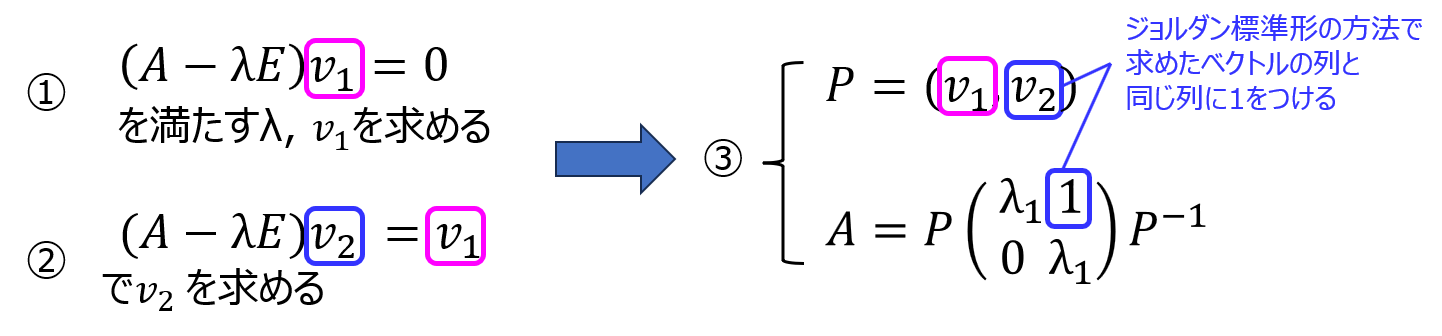
固有値を用いてある固有ベクトル\(v_{1}\)を求める
固有ベクトルを求めた連立方程式の右辺を0→固有ベクトルに変更し、もう一つのベクトル\(v_{2}\)を求める
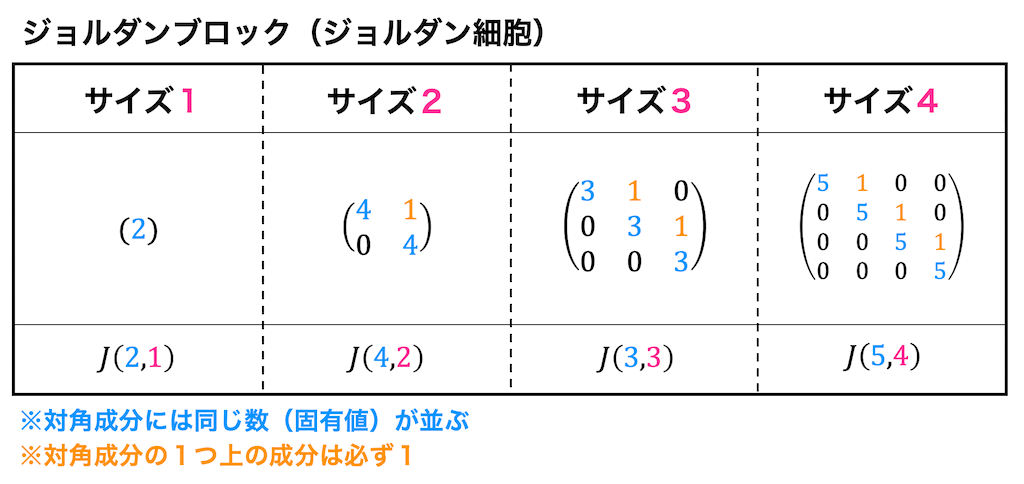
固有値が入る対角行列の重解を持つ部分の1つ上の要素に1を入れて、対角化する

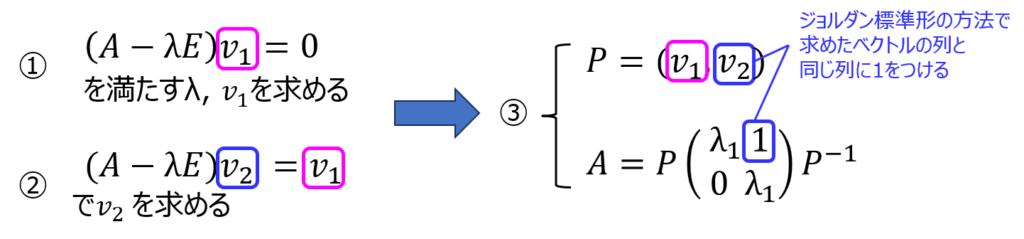
ジョルダン標準形による固有ベクトルの求め方を口語のように書くと上記のようになります。

こちらでなぜ求められるかの理由につきましては、ジョルダン標準形で検索下さると幸いです。

解答例

まず、行列\(A\)の固有値\((\lambda)\)を求めます。

\begin{align}&|A-\lambda E| \\ &=\begin{vmatrix} 1-\lambda & 1 \\ -1 & 3-\lambda \end{vmatrix}\\ &= \left( 1-\lambda \right) \left( 3-\lambda \right) +1 \\ &= \lambda^{2}-4\lambda+4 \\ &= (\lambda -2)^{2} \\ &=0 \end{align}

以上より、固有値\(\lambda =2\)(重解)

この時の固有ベクトルは、

\begin{eqnarray}\begin{cases}-x+y=1\\ -x+y=1\end{cases}\end{eqnarray}であるので、\(v_{1}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\)

Aを対角化するに必要なもう一つのベクトル\(v_{2}\)を考える。ジョルダン標準形の考え方により

\(\left( A-\lambda E\right) v_{2}=v_{1}\) が成立するので

\(\begin{pmatrix} -1 & 1 \\ -1 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\)

と書ける。これを整理すると、\(y=x+1\)のため、\(x=0\)と置くと、\(y=1\)

よって、\(v_{2}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}\)であることが分かった。

これより、行列\(P=\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}\)を定義し、逆行列\(P^{-1}=\begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix}\)とすると

与えられた行列\(A=\begin{pmatrix} 1 & 1 \\ -1 & 3 \end{pmatrix}\)は、下記のように対角化できる。

\(\begin{pmatrix} 1 & 1 \\ -1 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} 2 & 1 \\ 0 & 2 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix}\)

\(D=\begin{pmatrix} 2 & 1 \\ 0 & 2 \end{pmatrix}\)とし、\(D^{n}\)を考える。

\(D^{2}=\begin{pmatrix} 2^{2} & 2･2 \\ 0 & 2^{2} \end{pmatrix}\)

\(D^{3}=\begin{pmatrix} 2^{3} & 3･2^{2} \\ 0 & 2^{3} \end{pmatrix}\)より

\(D^{n}=\begin{pmatrix} 2^{n} & n･2^{n-1} \\ 0 & 2^{n} \end{pmatrix}\)であるので、\(A=PDP^{-1}\)をn個分右からかけていくと

\(A^{n}=PD^{n}P^{-1} \\ =\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} 2^{n} & n･2^{n-1} \\ 0 & 2^{n} \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix} \\ =2^{n}\begin{pmatrix} 1-\dfrac{n}{2} & \dfrac{n}{2} \\ -\dfrac{n}{2} & 1+\dfrac{n}{2} \end{pmatrix}\)

であることが分かった。