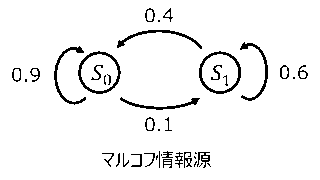
通信 マルコフ情報源の定常確率と遷移確率行列、エルゴート性
マルコフ情報源とは現在起こる状態が過去の状態に依存する情報源を言います。過去の状態に依存しない情報源を無記憶情報源(独立情報源)と言いますが、これとは反対の性質を示します。
通信
通信 
通信 相互情報量の意味、例題と通信路容量との関係
相互情報量とは事象A,Bの持つエントロピーの相互関係を示します。Aの持つ不確定性に対し、Bを受信することで明らかになった不確定性の量と解釈できます。
通信 【情報理論】情報源の情報量とエントロピーの計算問題
情報量とは情報の珍しさを示しています。確率\(P\)の情報源に対する情報量は以下で表されます。
通信 【通信工学】時分割多重伝送方式の原理と計算問題
時多重分割伝送方式(TDM)とはある信号をパルス波にして送信するとき、空き時間に別の信号を送信する方式です。(TDM：Time-division multiplexingの略です。)本伝送方式を用いることで、複数の信号を同じ通信路で送信することができます。
通信 PCM(パルス符号変調)伝送の原理とビットレートの計算問題
PCM伝送とは信号を0,1の2元情報符号列に変換し、パルス波として送信する方式です。(Pulse Code Modulationの略です。)
通信 白色雑音と入力信号のSN比(信号対雑音比)の求め方
白色雑音とは電力スペクトル密度\(N(f)\)が全ての周波数で一定の雑音を言います。時間領域\(t\)に落とし込むとインパルス関数になることから、ある時間で瞬間的に発生した雑音と言い換えることもできます。SN比とは入力信号\(s(t)\)から発生する電力\(P_{s}\)に対するノイズの電力\(P_{n}\)の比\(\frac{P_{s}}{P_{n}}\)を言います。
通信 パルス幅変調信号(APM)の原理と復元方法、問題
パルス幅変調(PAM)とはある周波数以下の信号を標本化し、周期Tごとに波形を持つ信号に変換することを言います。(PAM：Pulse Amplitude. Modulationの略です。)標本化した後の信号は、Tごとに決まった波形が出るため、帯域幅が\(\dfrac{1}{2T}\)の低域通過フィルタを用いれば、\(t=0\)の波形のみ復元できます。
通信 増幅器と総合利得、総合雑音指数の求め方。低減方法
総合利得、総合雑音指数とは複数の増幅器を直列で接続したとき、増幅器全体での利得を総合利得と言います。また、増幅器の入力部分のSN比\(SN1=\dfrac{S_{in}}{N_{in}}\)と出力部分のSN比\(SN2=\dfrac{S_{out}}{N_{out}}\)の比\begin{aligned}F=\dfrac{SN1}{SN2}\end{aligned}を総合雑音指数と言います。
通信 周波数変調(FM)の原理と電力効率、復調方法
周波数変調(FM)とは搬送波の周波数を変調信号\(s(t)\)に応じて変化させる方式です。(FM：Frequency Modulationの略です。)以前の記事では、搬送波の振幅を変化させる振幅変調(AM)を説明しました。振幅変調は、同一周波数帯でいくつもの信号を変調できる利点がありますが、電力効率が低いなどの欠点があります。
通信 振幅変調(AM)の原理、電力効率
送信したい変調信号\(s(t)\)に応じて搬送波の振幅を変化させることを言います。いま、上記左図のように搬送波\(A\cos(2\pi f_{c}t)\)が存在するとします。これに対し、変調指数\(m\)をかけた変調信号\(ms(t)\)を同じ正弦波で重ね合わせると、右図のように変化します。信号の受信側では、変調した信号の包絡線をなぞり(検波)、元の搬送波成分を打ち消すことで、変調信号を受け取ることができます。