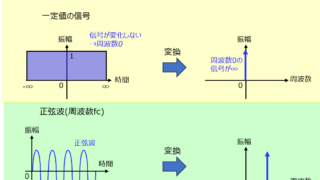
 通信
通信 院試でよく出るフーリエ変換の証明問題
フーリエ変換を出題する大学必須問題で不定期に出題:神戸大選択問題で毎年出題:東大(第3問)、阪大(電気系)、電通大(信号処理)選択問題で不定期に出題:京大(通信情報)、東北大(数学基礎)、農工大(数学)
 通信
通信 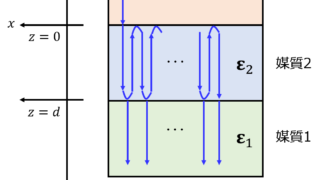 通信
通信 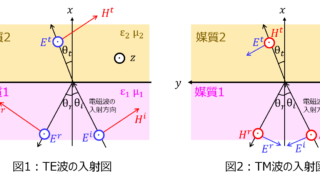 通信
通信 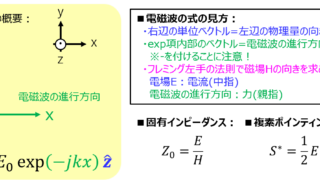 通信
通信 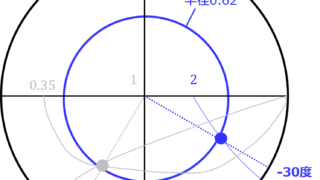 通信
通信 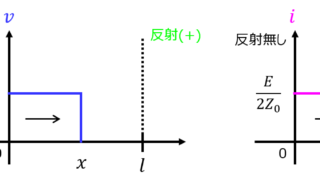 通信
通信 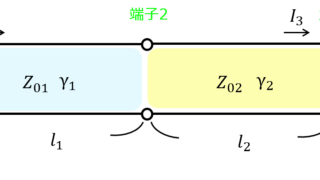 通信
通信 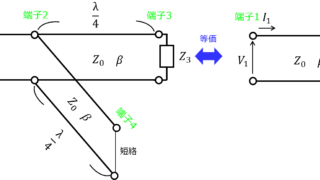 通信
通信 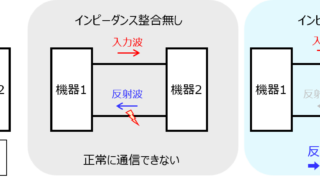 通信
通信 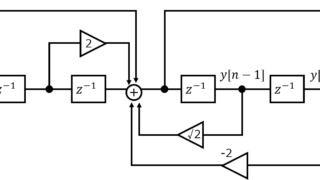 通信
通信