 電子回路
電子回路 CMOS(相補型トランジスタ)の動作原理と消費電力、特徴
相補型トランジスタとはPMOSとNMOSを直列に並べたトランジスタです。以前の記事で紹介したように、入力電圧が所定値以下のときは、PMOSが導通するので出力は上位の電圧になります。逆に所定値以上のときはPMOSは導通しなくなるので、出力電圧は0Vになります。
 電子回路
電子回路 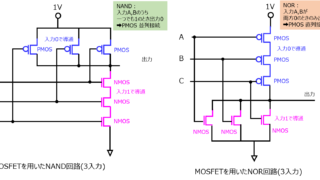 電子回路
電子回路 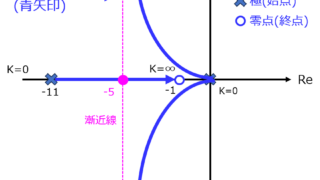 制御工学
制御工学 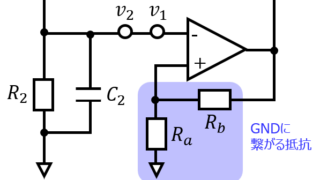 電子回路
電子回路 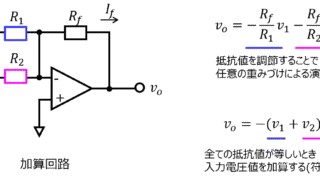 電子回路
電子回路  電子回路
電子回路  電子回路
電子回路  電子回路
電子回路  電子回路
電子回路  電子回路
電子回路