 量子・電子物性
量子・電子物性 【量子力学】トンネル効果の説明と反射率、透過率の導出と説明
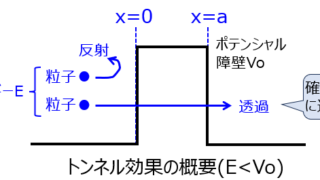
トンネル効果とは粒子がポテンシャル障壁を確率的に通過する現象を言います。例えば、ポテンシャル障壁\(V_{o}\)に対し、エネルギー\(E\)を持つ粒子が入射するとします。\(E<V_{o}\)の場合、古典力学の視点では、粒子は透過できず、...
 量子・電子物性
量子・電子物性  量子・電子物性
量子・電子物性  電子回路
電子回路  制御工学
制御工学  制御工学
制御工学 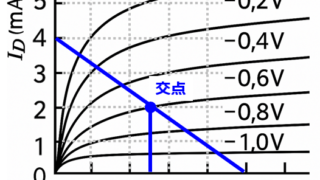 電子回路
電子回路 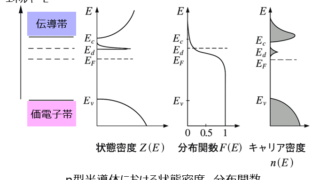 半導体デバイス
半導体デバイス 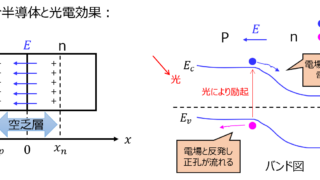 半導体デバイス
半導体デバイス 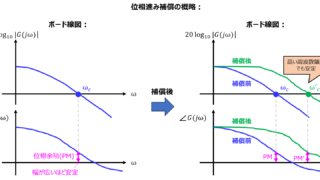 制御工学
制御工学  電子回路
電子回路