(1) 電気抵抗率ρで接地されていない無限に広く厚い平らな導体表面に、導電性プローブを点接触させ、電流を流す場合を考える。以下の問いに答えよ。
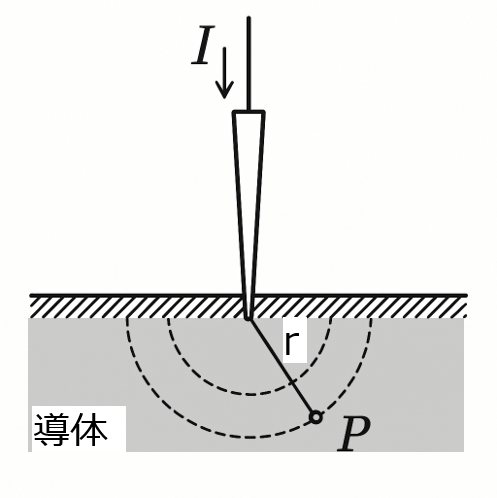
- 図1は、単独のプローブPから、この導体に電流Iを流すときの断面図である。プローブPの接触点から導体内の距離rの位置Pにおける電流密度\(J(r)\)を求めよ。ここで、導体は接触点から均一に流れ、同心円状表面(図1の破線面)の等電位面を作るものとする。
- 図1、点Pにおける電位\(V_{p}\)を求めよ。ただし導体は無限遠に存在するものとする。
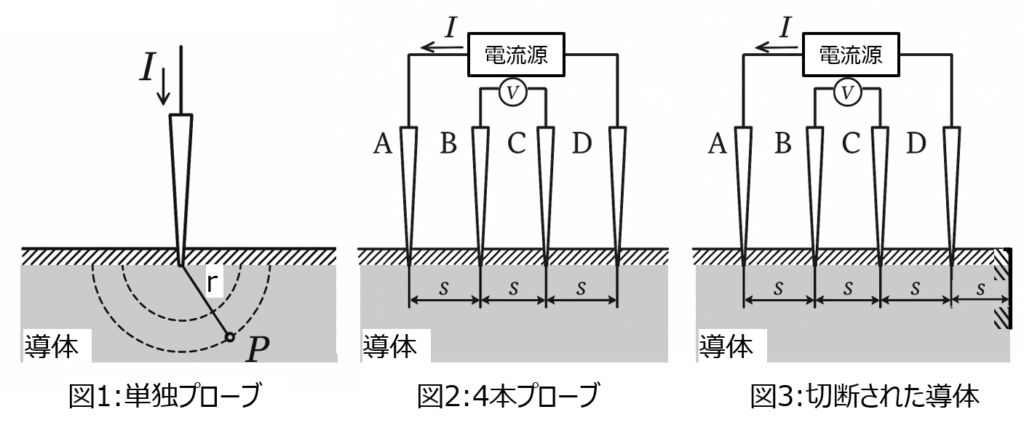
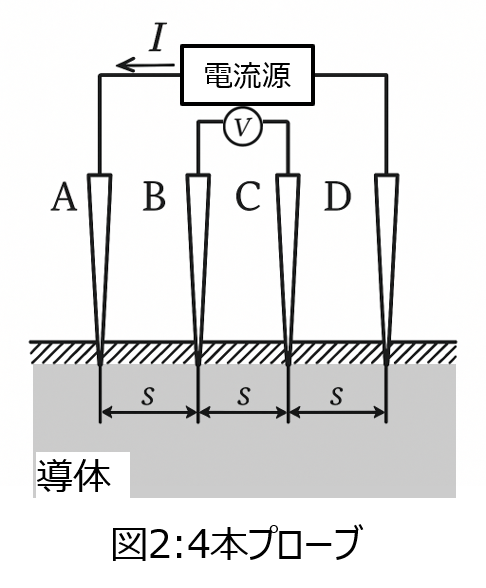
- 図2のように、4本のプローブA〜Dを等間隔に並べて、導体に接触させ、電流源からプローブA-D間に電流を流し、電圧計でB,C間の電圧\(V\)を計測する場合を考える。導体の電気抵抗率ρを求める式を電流I、プローブ間隔sを用いて導出せよ。
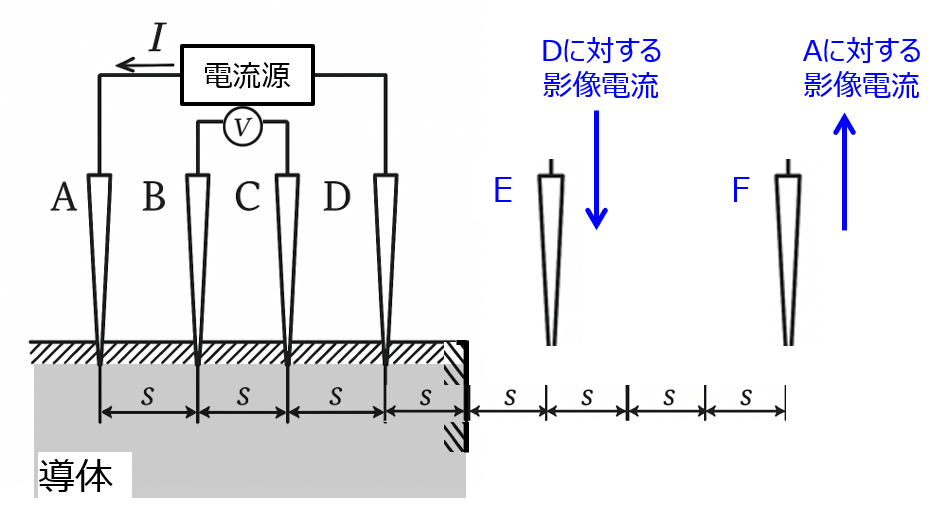
(2) 図3のように、この導体をプローブDの右側、距離sの位置で、プローブの接触面およびプローブ列と直交するように切断した場合を考える。この場合の電気抵抗率ρを表す式を導け。電流I、プローブ間隔sを用いて導出せよ。
名古屋大学大学院 電気電子情報工学科 2019年度院試問題 電磁気学 大問4より引用
四端子法とは
電気抵抗を正確に計測する手法の一つです。図2のように、計測対象の導体に対し、導電性のプローブを4つ接触させます。このとき、電流供給用の+-端子(計2つ。電流源)と、電圧計測用の+-端子(計2つ。電圧計)と端子を分けます。
電流供給用の端子から電流\(I\)を流し、その時の電圧\(V_{p}\)を専用の端子から計測すると、オームの法則により、その導体の電気抵抗\(R\)(電気抵抗率\(\rho\)でも良い)が求まります。
電流と電圧が1つの端子対で混在しないため、下記の利点があります。
- プローブの接触抵抗、電流源回路の抵抗を無視でき、電気抵抗率が精度よく求められる。
もし、2端子だけで抵抗率を計測する場合、電流源と同じ回路上で電圧\(V\)も計測する必要が出ます。(二端子法と言います。)
電流源の持つ内部抵抗を\(r\)とすると、電圧\(V\)の計測値は\(V=I(r+R)\)となります。rの量だけ誤差が発生します。計測対象の抵抗\(R\)が小さいほど影響を受けやすくなり、半導体材料、超伝導体などの抵抗率を計測する際は正しく計測できなくなります。
一方で、四端子法のように電流源と電圧計を別の端子対で分けた時はどうなるでしょうか。電圧計は、電流を流さなくて済むので内部抵抗を非常に大きくすることができます。この結果、電圧計に電流は殆ど流れ込まなくなるため、電圧を精度よく測定できます。
プローブから導体に電流を流した時の振る舞い
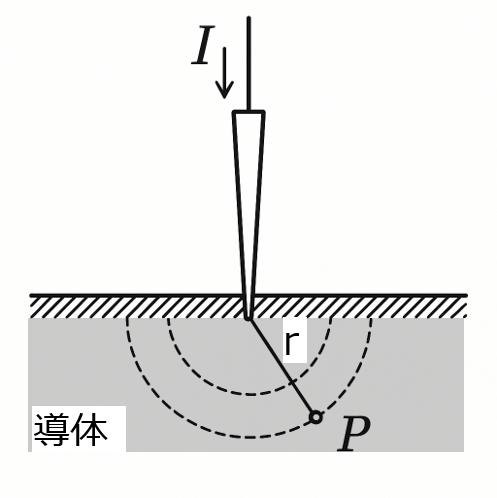
問題文より、電流源は導体に対し点接触しています。よって、接触点から放射状に電流が流れていると考えられます。
接触点から\(r\)離れた位置の電流密度\(J_{1}(r)\)は、半球の表面積\(2\pi r^{2}\)を用いると
\begin{aligned}J_{1}(r)=\dfrac{I}{2 \pi r^{2}}\end{aligned}
となります。電流源は回路として存在しているので、導体に流れ込む分は上式で表現できますが、一方で導体から電流源に戻る分の電流密度\(J_{2}(r)\)も考える必要があります。負の電流が流れる接触点から\(r\)離れた点では、上式の符号を逆にするだけでよく
\begin{aligned}J_{2}(r)=-\dfrac{I}{2 \pi r^{2}}\end{aligned}
になります。問題文で与えた端子B-Cの電位差を考えるうえでは、この2つの電流から発生する電位を重ね合わせて考える必要があります。
解答例
1.距離rの位置の電流密度
前節の説明により、\(J(r)=\dfrac{I}{2 \pi r^{2}}\)
2.点Pにおける電位
無限遠を基準点とする。\(J(r)=\sigma E =\frac{E}{\rho}\)より
\begin{aligned}E(r)=\dfrac{\rho I}{2 \pi r^{2}}\end{aligned}
であるから、上式を[-∞,r]で積分し
\begin{aligned}V_{p}&=-\int^{r}_{\infty} \dfrac{\rho I}{2 \pi r’^{2}}dr’ \\ &= \left[\dfrac{\rho I}{2 \pi r’}\right]^{r}_{\infty} \\ &=\dfrac{\rho I}{2 \pi r}\end{aligned}
3.電気抵抗率の計算
2.までで、端子1つに付き発生する電流密度、電位が分かりました。本問から、負の分の電流の概念が入るので、この分を足し合わせた結果が全体の電位になります。
端子AとDで発生する電場を重ね合わせ、端子B,C間の電位差を求める。まず、端子Bの電位\(V_{B}\)から考える。2.の結果のrに対し、端子AがBに及ぼす分はrにsを代入。端子DがBに及ぼす分はrに2sを代入すれば良いので
\begin{aligned}V_{B}&=\dfrac{\rho I}{2 \pi s}-\dfrac{\rho I}{4 \pi s} \\ &=\dfrac{\rho I}{4 \pi s}\end{aligned}
次に、端子Cの電位\(V_{C}\)を考える。端子Aからは距離2s、端子Dからは距離s離れているので
\begin{aligned}V_{C}&=-\dfrac{\rho I}{2 \pi s}+\dfrac{\rho I}{4 \pi s} \\ &=-\dfrac{\rho I}{4 \pi s}\end{aligned}
以上から、端子B-C間の電位差\(V\)は
\begin{aligned}V=\dfrac{\rho I}{2 \pi s}\end{aligned}
これを\(\rho\)に関して変形すると、求める電気抵抗率は
\begin{aligned}\rho = 2 \pi s \dfrac{V}{I}\end{aligned}
(2)切断された導体で計測したときの電気抵抗率
図を見て気づいた方もいらっしゃるかもしれませんが、鏡像法を用います。導体の切れ目を境に端子A,Dと対称な位置E,Fに逆向きの電流Iを流します。(下図)
電位を重ね合わせる個数が2.では2つだったのが、本問では4つとなります。少し計算は複雑となりますが、内容は変わりません。
まず、端子Bの電位\(V_{B}\)について、端子Eからは距離4s、端子Fからは距離7s離れているので
\begin{aligned}V_{B}&=\dfrac{\rho I}{2 \pi s}-\dfrac{\rho I}{4 \pi s}+\dfrac{\rho I}{2 \pi 4s}-\dfrac{\rho I}{4 \pi 7s} \\ &=\dfrac{17 \rho I}{56 \pi s}\end{aligned}
次に端子Cの電位\(V_{C}\)について、端子Eからは3s、端子Fからは6s離れているので
\begin{aligned}V_{C}&=\dfrac{\rho I}{2 \pi 2s}-\dfrac{\rho I}{2 \pi s}+\dfrac{\rho I}{2 \pi 3s}-\dfrac{\rho I}{4 \pi 6s} \\ &=-\dfrac{\rho I}{6 \pi s}\end{aligned}
端子B-C間の電位差\(V\)は
\begin{aligned}V&=\dfrac{51\rho I+ 28 \rho I}{168 \pi s} \\ &=\dfrac{79 \rho I}{168 \pi s}\end{aligned}
以上より、求める電気抵抗率は
\begin{aligned}\rho=\dfrac{168}{79}\pi s \dfrac{V}{I}\end{aligned}
2.の結果は\(2 \pi s = \frac{158}{79} \pi s \)でしたが、本問では\(\frac{10}{79}\)分誤差が発生しています。
上記の結果から、導体を計測するときは、なるべく中心の位置に端子を設置し、鏡像電荷の影響を最小限にすることが必要と分かりました。