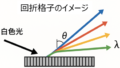
下記のように、焦点距離が$f$の薄肉凸レンズが距離$d$の間隔で無数に置かれている。光線を入射するとき、下記の問いに答えよ。
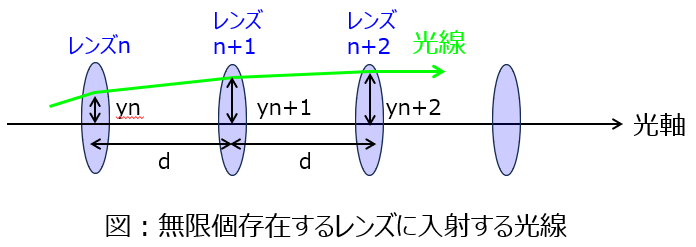
問1:$n$番目のレンズを通過する光線の縦軸方向の距離を$y_n$とするとき、$y_n,y_{n+1},y_{n+2}$の関係を求めよ。
問2:指数関数型の解$y_n=Ae^{in\theta}$を仮定し、光線が光軸を逸れることなく進行するための$d,f$に関する条件を求めよ。
凸レンズとは
中心が厚く、ある一点(焦点)に光を集める性質のある透明体を言います。中心部分ではほぼ平面に近く、光は殆ど曲がらないですが、端部では斜面になっているため、入射光は焦点へ屈折します。
凸レンズに対する入射光線のy座標を$y_{in}$、接線成分を$dy/dz=y’_{in}$、出射光線のy座標を$y_{out}$、接線成分を$dy/dz=y’_{out}$とすると、下記の関係があります。
\begin{aligned}\begin{pmatrix}y_{out} \\ y’_{out}\end{pmatrix}=\begin{pmatrix} 1 & 0 \\ -1/f & 1\end{pmatrix}\begin{pmatrix}y_{in} \\ y’_{in}\end{pmatrix}\end{aligned}
なお、第二式は下記の図により導出できます。
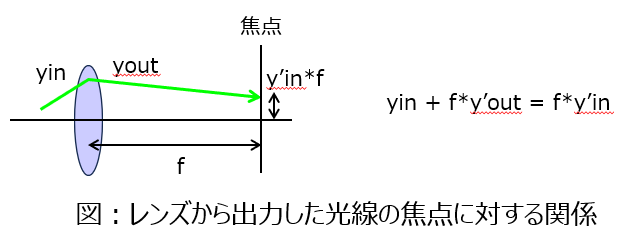
上式は薄レンズの前提で成立します。厚レンズの場合、レンズ内の光路を無視できないため、その分を式に加える必要があります。
問題を解くうえでの留意点
凸レンズが一つだけなら式(1)を一度適用するだけで良いですが、本問は無数に存在しています。
よって、ある凸レンズを出た光が次の凸レンズに対してどのように影響するのかを一般化する必要があります。
凸レンズを出た光線は次の凸レンズまで距離$d$あることから、下記の関係になります。
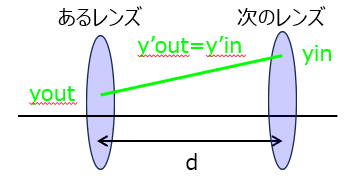
\begin{aligned}\begin{pmatrix}y_{out} \\ y’_{out}\end{pmatrix}=\begin{pmatrix} 1 & d \\ 0 & 1\end{pmatrix}\begin{pmatrix}y_{in} \\ y’_{in}\end{pmatrix}\end{aligned}
高校数学の座標系に関する知識(一次関数)のため、詳しい説明は割愛します。
結局、式(1)(2)を合わせることで、$n$番目のレンズに入射する光と、$n+1$番目のレンズに入射する光には下記の関係があります。
\begin{aligned}\begin{pmatrix}y_{n+1} \\ y’_{n+1}\end{pmatrix}=\begin{pmatrix} 1 & 0 \\ -1/f & 1\end{pmatrix}\begin{pmatrix} 1 & d \\ 0 & 1\end{pmatrix}\begin{pmatrix}y_{n} \\ y’_{n}\end{pmatrix}\end{aligned}
\begin{aligned}\begin{pmatrix}y_{n+1} \\ y’_{n+1}\end{pmatrix}=\begin{pmatrix} 1 & d \\ -1/f & (1-d/f)\end{pmatrix}\begin{pmatrix}y_{n} \\ y’_{n}\end{pmatrix}\end{aligned}
$n$を$n+1$にした場合も考え、問1を考えていきます。
解答例
問1:凸レンズnとn+2の関係
式(4)の第2式をn→n+1にすると
\begin{aligned}y’_{n+1}=\dfrac{1}{d}(y_{n+2}-y_{n+1})\end{aligned}
式(4)の第2式を上式に代入すると
\begin{aligned}y_{n+2}-(2-d/f)y_{n+1}+y_{n}=0\end{aligned}
問2:光線が外れない条件
$y_n=Ae^{in\theta}$を問1の結果に代入すると
\begin{aligned}e^{i2 \theta}-(2-d/f)e^{i \theta}+1=0\end{aligned}
\begin{aligned}e^{i \theta}=\dfrac{1}{2}(2-d/f)±i\sqrt{1-(2-d/f)^{2}}\end{aligned}
$\theta$が実数のとき、位相ずれが発生せず、光線が大きく外れることなく進行する。これを満たすには、√内が正であれば良いので
\begin{aligned}1-(2-d/f)^{2}≧0\end{aligned}
\begin{aligned}0≦d≦4f\end{aligned}