波長$\lambda$の単色平面波の回折について以下の問いに答えよ。スリットはxy平面内にあり、z軸となす角$\theta$は1より十分小さいとし、$\sin\theta \sim \theta$とする。
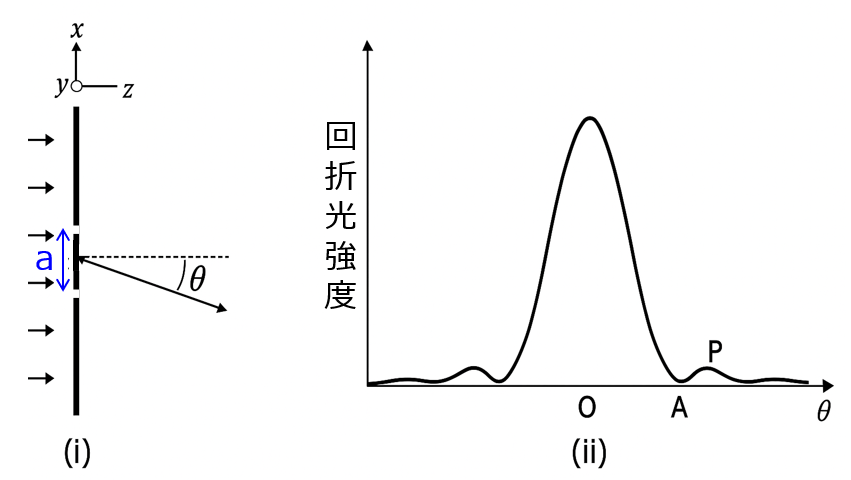
(a)図(i)のように、x軸方向の幅が$a$でy軸方向には十分長いスリットに、垂直に平面波が入射している。この時スリットから十分遠方の回折光強度分布は図(ii)のようになった。回折光強度が0となる点Aでの回折角$\theta$を求めよ、また、最大強度の次の強度ピークPの回折角$\theta$を求めよ。ここで、方程式$\alpha=\tan \alpha$の解は$\alpha=0,±4.49…$であることを用いて良い。
電気通信大学 2021年8月 基盤理工学 大問2より抜粋
回折格子とは
光を複数のスリットにより分解し、干渉を利用して波長ごとに異なる方向に光を分散させる光学素子です。分光器やレーザーの波長選択装置など、様々な工学分野に用いられています。本問では、簡単化のため、一つの波長しか存在しない単色平面波が2つの穴から回折する場合について考えます。
回折格子の性質
干渉光条件
溝の間隔を$a$、回折角を$\theta$、光の波長を$\lambda$とすると、それぞれの溝から出てくる光の光路差は$a \sin\theta$となります。これが波長の整数倍で強め合いますので、強い干渉光は下記の条件で得られます。
\begin{aligned}a \sin \theta=n \lambda\end{aligned}
強度
干渉条件に関しては、高校物理の教科書でも出てくる内容のため、分かる人が多いかもしれません。一方で、強度に関しても院試では出題されることが多いです。
単一スリットの回折格子の光強度分布($\theta$依存性)は下記の式で表されます。
\begin{aligned} I(\theta)=I_0 \left( \frac{\sin(\frac{\pi a \sin\theta}{\lambda})}{\frac{\pi a \sin\theta}{\lambda}} \right)^2\end{aligned}
丸暗記でも良いですが、導出手順も下記に示します。結論、フーリエ変換の知識を用います。
回折した光の振幅をフーリエ変換で考えます。複素振幅$A(\theta)$で表し、光のスリットの間隔を-a/2~a/2で考えて
\begin{aligned}A(\theta)& \propto \int_{-a/2}^{a/2} e^{iky’ \sin\theta} dy’ \\ &=\left[ \frac{e^{iky’ \sin\theta}}{ik \sin\theta} \right]_{-a/2}^{a/2}\\ &= \frac{e^{ik(a/2)\sin\theta} – e^{-ik(a/2)\sin\theta}}{ik \sin\theta}\end{aligned}
オイラーの公式を用いて
\begin{aligned}A(\theta) &\propto \frac{2i\sin(k(a/2)\sin\theta)}{ik \sin\theta} \\&= \frac{2\sin\left(\frac{2\pi}{\lambda}\frac{a}{2}\sin\theta\right)}{\frac{2\pi}{\lambda}\sin\theta}\end{aligned}
スリットの中心における振幅を $A_0$ とすると、
\begin{aligned}A(\theta) = A_0 \frac{\sin\left(\frac{\pi a \sin\theta}{\lambda}\right)}{\frac{\pi a \sin\theta}{\lambda}}\end{aligned}
光強度$ I_{\theta}$は$A(\theta)$の2乗の絶対値で表されるため(2式)で表される。なお、\(I_{0}=A_{0}^{2}\)である。
解答例
(a)回折角の算出
(1式)を変形し、求める回折角\(\theta\)は
\begin{aligned}\sin \theta=\dfrac{n \lambda}{a}\end{aligned}
$ \sin\theta \propto \theta$と近似できるので
\begin{aligned} \theta=\dfrac{n \lambda}{a}\end{aligned}
次に、最大強度の次のサイドピークPの回折角$\theta$を求める。光強度の最大値は、$\frac{\mathrm{d}I}{\mathrm{d}\theta} = 0$となる点を考えれば良い。
$\alpha = \frac{\pi a \sin\theta}{\lambda}$ とおくと、$I(\alpha)=I_{0}\left(\frac{\sin \alpha}{\alpha}\right)^{2}$ とおける。
変数部分をを$ \alpha $で微分し、=0の条件を考えると
\begin{aligned}\dfrac{d}{d \alpha}\left(\frac{\sin \alpha}{\alpha}\right)^{2}\end{aligned}
\begin{aligned}2 \left( \frac{\sin\alpha}{\alpha} \right) \frac{\alpha \cos\alpha – \sin\alpha}{\alpha^2} = 0\end{aligned}
$ \frac{\sin \alpha}{\alpha} \neq 0 $のため
\begin{aligned}\alpha \cos\alpha – \sin\alpha=0\end{aligned}
これを整理すると$ \tan \alpha = \alpha $
問題文より、tanα=αの解は$\alpha = 0, \pm 4.49, \dots$になる。 $\alpha = 0$は中央最大値に対応し、 次のサイドピークは、$\alpha = \pm 4.49$に対応する。
$\frac{\pi a \sin\theta}{\lambda} = \pm 4.49 \sin\theta \approx \theta$と近似すると、
\begin{aligned}λπaθ=±4.49\end{aligned}
\begin{aligned}θ=±πa4.49λ\end{aligned}
最後に
本問の続きに、3つのスリットに光波が入射したときの強度を考える問題があります。単スリットの重ね合わせで考察することができますので、興味がある方はチャレンジしてみてください。