 電気回路
電気回路 【電気回路】補償定理の性質を例題を用いて解説
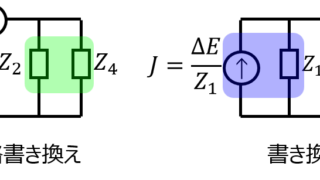
補償定理とは電流が流れている枝にインピーダンス\(\Delta Z\)を接続したときに発生する電流は、回路に接続されている電源を全て殺し、電流の向きと反対にの電圧源を接続したときに流れる電流に等しいことを言います。
 電気回路
電気回路  電気回路
電気回路 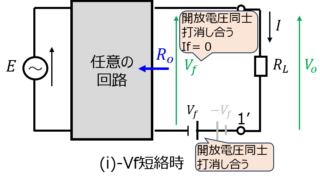 電気回路
電気回路 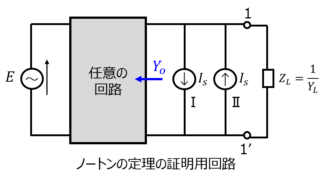 電気回路
電気回路 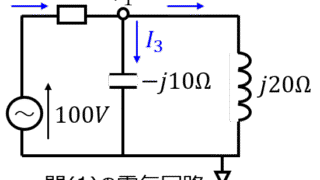 電気回路
電気回路  電気回路
電気回路  電気回路
電気回路 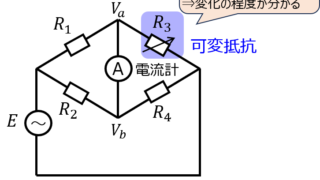 電気回路
電気回路 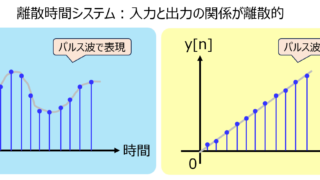 通信
通信 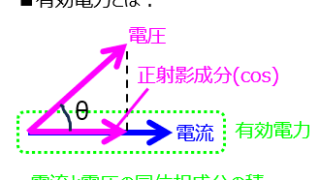 電気回路
電気回路