 電気回路
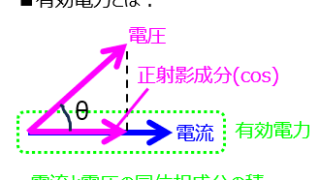
電気回路 有効電力、無効電力とは?力率との関係を例題を用いて解説
問題(1)ある回路に流れる電流、電圧がそれぞれ下記の式で表される。複素電力、皮相電力、有効電力、無効電力、力率を求めよ。\begin{cases}v(t)=100\sqrt{2}\sin(120\pi t +\frac{5}{18}\pi)...
 電気回路
電気回路  電気回路
電気回路 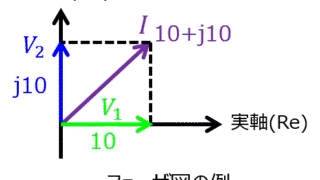 電気回路
電気回路 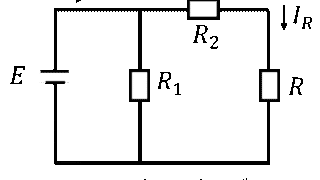 電気回路
電気回路 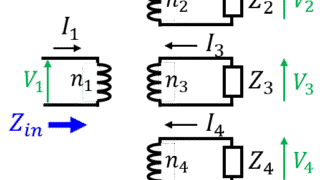 電気回路
電気回路 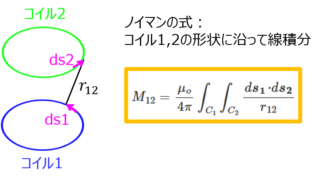 電磁気学
電磁気学 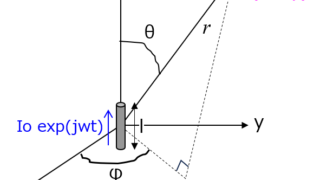 通信
通信  電気回路
電気回路  電磁気学
電磁気学  コラム
コラム