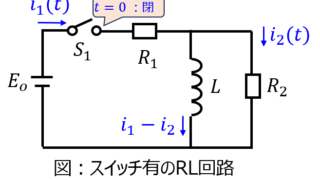
 電気回路
電気回路 【過渡現象】初期値の定理、最終値の定理と電流の極限
初期値(最終値)の定理とはラプラス変換(s領域)のまま、時間領域(t=0)の値、(t=∞)の極限を求めることができる方法です。ラプラス変換した関数にsを乗算し、時間領域と逆向きの極限を考えることで、求めたい原関数の値を求められることを意味しています。
 電気回路
電気回路 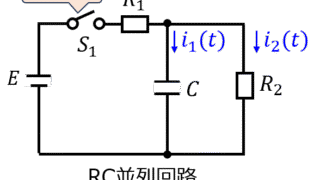 電気回路
電気回路 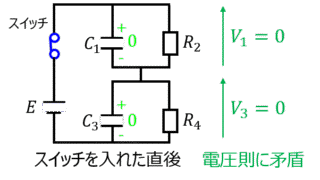 電気回路
電気回路 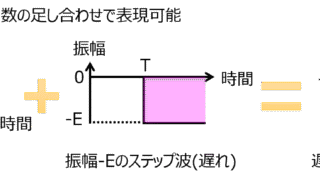 電気回路
電気回路  電気回路
電気回路  電気回路
電気回路  電気回路
電気回路  電気回路
電気回路  電気回路
電気回路  電気回路
電気回路