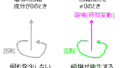可動コイル型電流計と正接電流計の計測原理

はじめに

本問は、院試ではあまり出ません。電験対策用の記事になります。毎年、理論科目で1問程度計測器に関する問題が出題されます。他の問題で点が取れるなら大丈夫ですが、ボーダーライン上に居る方はこの1問が合否を分ける場合があります。頭の片隅に置いておくと吉です。

直流電流計

記事の題名にした電流計は、直流を計測するための電流計になります。交流専用の電流計、交直両用のものもありますが、本記事では、直流電流計を説明します。

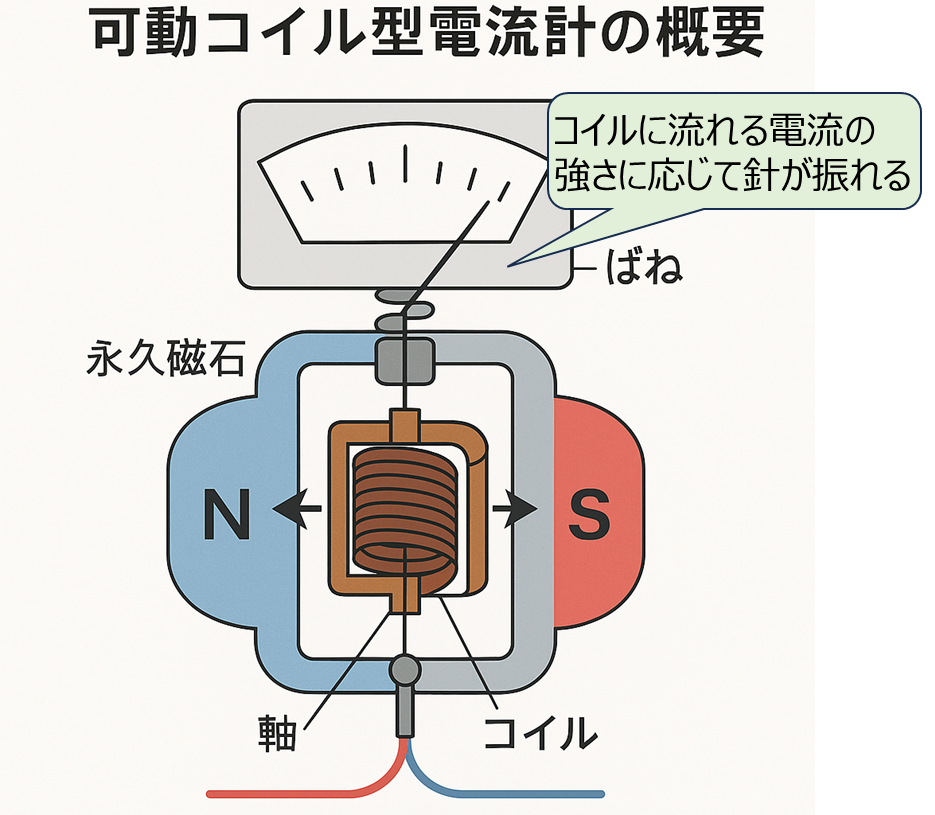
可動コイル型電流計

永久磁石(N,S極)の間に回転できる可動コイルを設置する構成です。可動コイルに計測したい電流を流すと、電磁力によりコイルが回転します。電磁力は可動コイルに流す電流に比例することから、回転の大きさによって、計測する電流の値が分かるということですね。

交流の場合、電磁力が時間によって正負の方向に振れるため、使用することができません。

回路記号としては下記になります。U字型で覚えると良いでしょう。

可動コイルの支え方

ピボット方式とトートバンド方式があります。

ピボット方式は、軸受けに可動コイルを固定し、指針が回転する構成です。応答性に優れています。

トートバンド方式は、釣り線に可動コイルを固定する方式です。機械的な摩擦が最小限になるため、正確に計測できることや、衝撃や振動に強い利点があります。

正接検流計

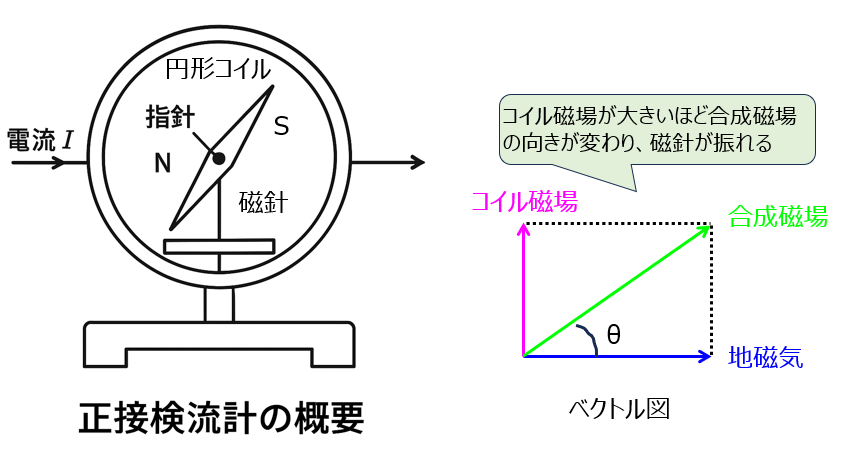
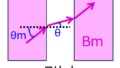
地磁気に対し垂直な磁場がかかるように配置した円形コイルの中心部に小磁針を置いた構成です。

円形コイルに電流を流すと、下記のような磁場分布、合成磁場になります。

コイルの磁場が大きいほど、合成磁場が図上：Y軸方向に強くなり、小磁針の振れる向きも変わります。

合成磁場の方向

前章の図において、\(\theta\)を設定する。地磁気を\(H_{o}\)、円形コイルの磁場を\(H_{1}\)、半径を\(a\)とする。アンペールの法則より、\(H_{1}=\frac{NI}{2a}\)で表されるため

\begin{aligned}\tan\theta &=\dfrac{H_{1}}{H_{o}} \\ &=\dfrac{NI}{2aH_{o}}\end{aligned}

\begin{aligned}\theta=\tan^{-1}\left(\dfrac{NI}{2aH_{o}}\right)\end{aligned}

で表されます。小磁針も、合成磁場の方向を向いて止まるため、上記の関係式になります。

例題1

<解答例>

(1)式に与えられたパラメータを代入し

\begin{aligned}\tan(30°)&=\dfrac{20 I}{2･10･30} \\ I&=\dfrac{1}{\sqrt{3}}･30 \\ &=10 \sqrt{3}[A]\end{aligned}

例題2

<解答例>

(1)式を変形し、\(\theta\)で微分する。

\begin{aligned}I=\dfrac{2aH_{o}}{N}\tan\theta\end{aligned}

\begin{aligned}dI=\dfrac{2aH_{o}}{N}\dfrac{1}{\cos^{2} \theta}d\theta\end{aligned}

\begin{aligned}\dfrac{dI}{I}&=\dfrac{d \theta}{\cos^{2} \tan\theta} \\ &=\dfrac{d\theta}{\sin \theta \cos\theta} \\ &=\dfrac{2d\theta}{\sin 2\theta}\end{aligned}

\(\sin 2\theta\)が最大のとき、分母が最大となり相対誤差も小さくなる。このため、\(\theta=45°\)になるように振れ角を設定すれば良い。

参考文献

詳解物理学演習(下) 後藤憲一(著) P208-210