マルコフ情報源の定常確率と遷移確率行列、エルゴート性

問題

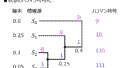
下記の図で表されるマルコフ情報源についての問いに答えよ。

(1)遷移確率行列を求めよ。
(2)定常確率を求めよ。
(3)この情報源のエントロピーを求めよ。
(4)この情報源はエルゴート的であるか判別せよ。

マルコフ情報源とは
定常確率について
マルコフ情報源のエントロピーの求め方
エルゴート性について
解答例
参考文献

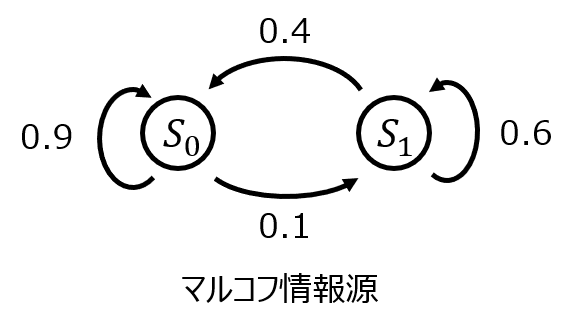
マルコフ情報源とは

現在起こる状態が過去の状態に依存する情報源を言います。

過去の状態に依存しない情報源を無記憶情報源(独立情報源)と言いますが、これとは反対の性質を示します。

マルコフ情報源の例

過去の状態に依存することから、状態遷移を考えると複数の状態が存在すると考えられます。

問いで示されている情報源がまさにそうです。\(S_{0}\)に遷移する確率を考えると、現状態が\(S_{0}\)なら0.9、\(S_{1}\)なら0.4の確率になります。

このように、依存する状態の数に応じて、複数の状態が存在します。

状態遷移先、確率の関係は、遷移状態行列で示されます。

左辺が現状態、右辺を遷移先とし、遷移確率の関係を行列表示したものです。

\begin{aligned}\begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix}=\begin{pmatrix} 0.9 & 0.1 \\ 0.4 & 0.6 \end{pmatrix}\begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix}\end{aligned}

なお、状態毎の遷移確率の合計は1になることから

\begin{aligned}p_{0}+p_{1}=1\end{aligned}

の関係も存在します。(1)式を解いて\(P_{0}\)と\(P_{1}\)の関係を求めた後、(2)式を用いて具体的な値を求めるわけですね。

無記憶情報源の例

過去の記事の例題がそうです。確率の等しいサイコロを複数回振るとき、それぞれの試行時の出目は過去の状態に依存しません。

このため、状態的には一つで、与えられた確率をそのまま使用し、エントロピーなどの各種パラメータを求めます。

定常確率について

マルコフ情報源の状態遷移を繰り返した時、最終的に各状態が行きつく確率を言います。

定常確率の求め方

前章にヒントが出ていますが、状態遷移行列(1)式と確率の(2)式を連立して解けば求められます。

\begin{cases}p_{0}=0.9p_{0}+0.1p_{1}\\ p_{1}=0.1P_{0}+0.6p_{1}\\ 0=p_{0}+p_{1}\end{cases}

これだけ見ると、ある状態を与えた時の次の状態を求めているに過ぎないです。極限を求めているように見えないですが、なぜこの式を解くだけで良いのでしょうか。

感覚的な理解ですが、下記の解釈ができます。

左辺が定常確率(極限分布)ならば、次回の遷移をした後も同じ分布を取る。よって、左辺と右辺をただ等号で結べば良い。

数式的な証明もできますが、試験問題を解くうえでは、こちらの理解で問題無いと思います。

マルコフ情報源のエントロピーの求め方

以前の記事で紹介した下記の式を用います。

\begin{aligned}H\left( A| B\right) =-\sum_{A}\sum_{B}P\left( a,b\right) \log P\left( a|b\right)\end{aligned}

事象Bが分かっている状況下での事象Aの条件付きエントロピーを示しています。

本記事の場合、事象Bは現在の状態を表し、事象Aは遷移先の状態を表します。

このように、複数の状態遷移が絡むマルコフ情報源のエントロピーを求める際は、条件付き確率を使用することが必要です。必ず忘れないようにしましょう。

現在の状態については、前節で説明した定常確率を代入すれば良いです。そこからの状態遷移先は、遷移確率行列に基づいて判断すれば良いです。

問題を解くうえでは、下記の式を用います。(\(p_{0}(\infty),p_{1}(\infty)\)は、それぞれの定常確率。\(p_{00}\)は、遷移確率行列の(0,0)成分。\(p_{01}\)以降もそれぞれ対応する成分を表します。)

\begin{aligned}H\left( A| B\right) =-(p_{0}(p_{00}\log_{2}p_{00}+p_{01}\log_{2}p_{01})+p_{1}(p_{10}\log_{2}p_{10}+p_{11}\log_{2}p_{11}))\end{aligned}

エルゴート性について

文献によって、いくつか定義が分かれますが、本記事では下記2点について説明します。

情報源に消散部分が無いこと
情報源に周期性が無いこと

1.について、ある情報に遷移したら、そこから抜け出せない状態が無いことを示しています。
2.について、遷移先が一意に定まり、決まった規則で遷移し続ける情報源を言います。

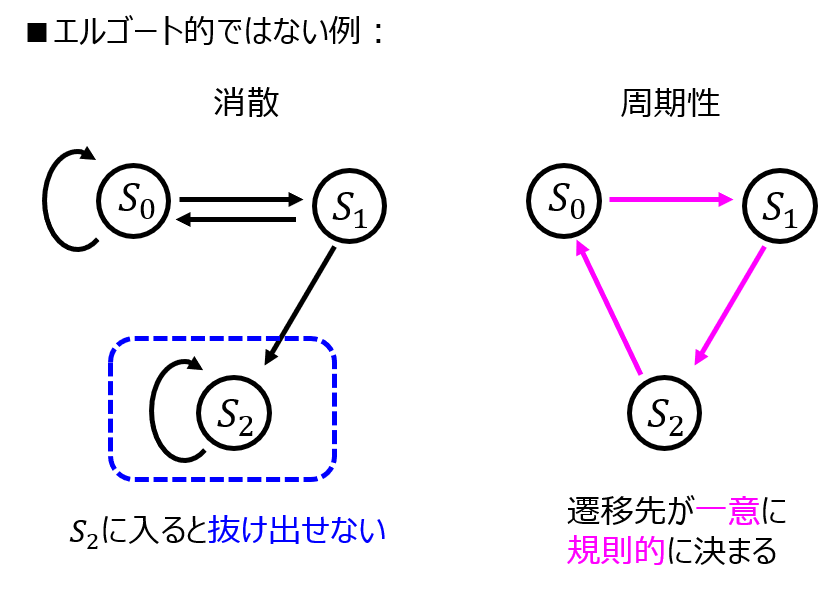
1.2.いずれにも該当しない本記事の問いの情報源はエルゴート的だと予想できます。

注意：エルゴート的である他の必要条件

文献によっては、情報源の定常分布と時間平均分布が一致することもエルゴート性の条件として説明しています。

これは、前章で説明した定常分布で得た結果と、下記に示す時間平均分布

\begin{aligned}\boldsymbol{p(\infty)}=\lim _{t+\infty }\dfrac{1}{t}\left( \boldsymbol{p}+\boldsymbol{p^{2}}+\ldots +\boldsymbol{p^{n}}\right)\end{aligned}

の計算結果が一致することを言います。

試験問題でエルゴート性が問われている際は、時間平均分布に関する問いが含まれているかどうかで議論の程度を変えた方が良いと思います。

基本的に、(7)式を計算することは大変なケースが多いです。限られた試験時間中に実施することはリスクだと考えています。

採点者次第で減点されるかもしれませんが、基本的にCHECKで記載したことを根拠に説明する方が試験全体を見ても最適かと思います。

(※最終判断は読者の皆様に委ねます。毎回説明を省略することを推奨しているわけではありません。時間平均分布に関する問題を出題する際、計算しやすい行列で出てくることが多いので、出題者の意図を汲みとった解き方を目指すと上記方針に落ち着くのでは。と管理人は考えます。)

解答例

(1)遷移確率行列

前章までの説明より、与えられた状態遷移図を行列表示すれば良い。

\begin{aligned}\begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix}=\begin{pmatrix} 0.9 & 0.1 \\ 0.4 & 0.6 \end{pmatrix}\begin{pmatrix} p_{0} \\ p_{1} \end{pmatrix}\end{aligned}