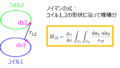下記の系における分極電荷をそれぞれ求めよ。
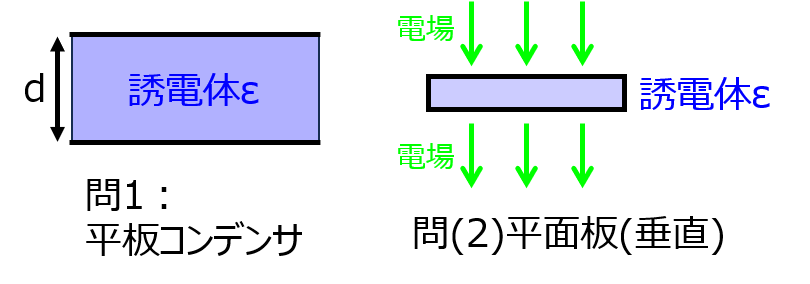
(1)誘電率\(\varepsilon_{o}\)の誘電体を挿入した平行平板コンデンサにおいて、誘電体表面に発生する分極電荷密度
(2)外部電場\(\boldsymbol{E_{o}\)が無限に広い誘電体の平板に垂直にかかっている。誘電体表面で発生する分極電荷密度
(3)(2)において、外部電場が誘電体の平板に平行にかかる場合はどうなるか。
(4)電荷Qを持つ半径aの導体球が無限に広がっている誘電体(誘電率\(\varepsilon\))の中に置かれている。誘電体と導体球の間で発生する分極電荷の量。

分極電荷とは
誘電体内部で発生する正負に分かれた電荷の群を言います。
電場が誘電体にかかっている系を考えます。誘電体は、マクロで見れば電気的に中性です。しかし、電場によって内部の電子が吸い寄せられます。その結果、ミクロで見れば負の領域と正の領域が発生します。
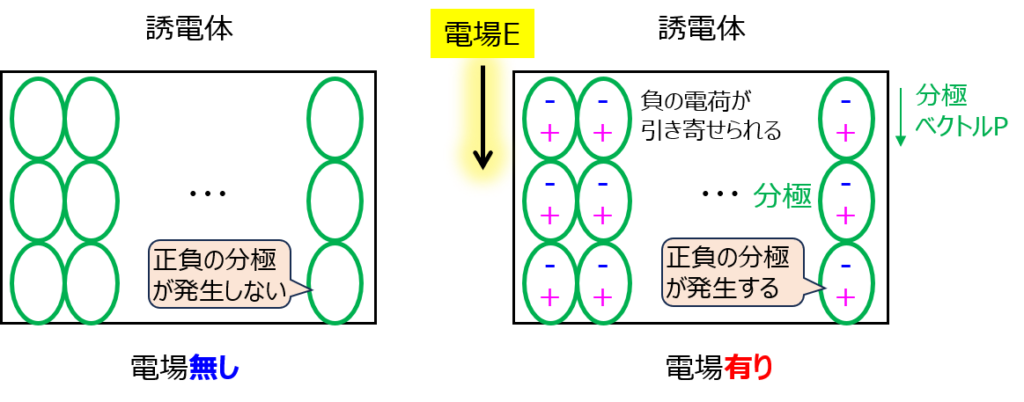
この現象を分極と言い、分極により発生する電荷量を分極電荷と言います。
また、正負の分極電荷を結ぶベクトルを分極ベクトルと言います。分極ベクトルには下記の物理的意味があります。
- 単位体積当たりの双極子モーメントの大きさ
- 分極ベクトル\(\boldsymbol{P})に垂直な単位面積を通過する正電荷の量
これは、次節のように、分極ベクトルと分極電荷の面密度、体積密度の関係式を導くときに重要な考え方になります。
分極ベクトルと分極電荷密度の関係
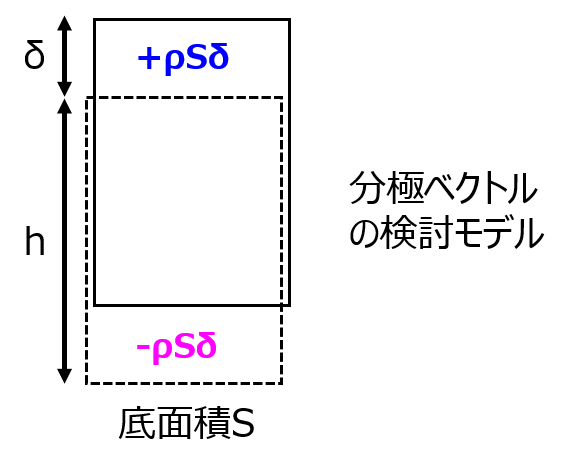
上記の分極モデルを考えます。分極電荷密度\(\rho\)、底面積\(S\)、高さ\(h\)の直方体を考えます。正の分極電荷を持つ領域と、負の分極電荷を持つ領域が微小ベクトル\(\boldsymbol{\delta}\)だけずれています。
この時、分極電荷は\(\sigma_{p}=\rho S \delta\)になります。
双極子モーメントは、上式に電荷同士が離れている距離\(h\)をかけると良いので
\begin{aligned}\rho S \delta ・h=\rho \delta *V\end{aligned}
になります。(Vは体積で、V=Shです。)
よって、前節のCheckボックス1.の説明内容により、単位体積当たりの双極子モーメントの大きさは
\begin{aligned}\boldsymbol{P}=\rho \delta\end{aligned}
次に、Checkボックス2により、ずれ\(\delta\)により表面から飛び出す正電荷の量は、分極ベクトル\(\boldsymbol{P}\)に等しいので
\begin{aligned}P=\sigma_{p}\end{aligned}
となります。(2)式と合わせると、\(P=\sigma_{p}=\rho \delta\)となり、分極電荷の面密度、体積密度の間の関係式も導かれました。
分極電荷の求め方
電束密度と電場、分極ベクトルの関係式
\begin{aligned}\boldsymbol{D}=\varepsilon_{o}\boldsymbol{E}+\boldsymbol{P}\end{aligned}
とガウスの法則を連立して求めることが多いです。
電束密度に関するガウスの法則では、真電荷の面密度を\(\sigma\)とすると、
\begin{aligned}D=\sigma\end{aligned}
\begin{aligned}P=\sigma_{p}\end{aligned}
なる関係式が導かれます。問題で与えられている系ごとに電束密度、電場を考えて(4)式に代入すると分極電荷の面密度を求めることができます。
解答例
(1)平行平板コンデンサ
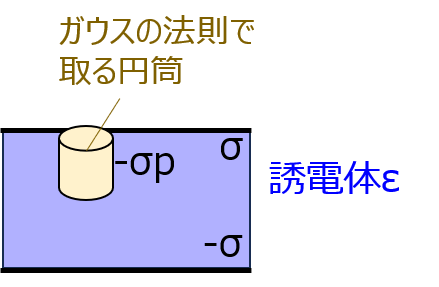
導体極板と誘電体にまたがる底面積Sの円筒を考える。ガウスの法則により
\begin{aligned}DS=\sigma S \\ D=\sigma\end{aligned}
誘電体内部の電場は、誘電率が\(\varepsilon\)なので
\begin{aligned}E=\dfrac{\sigma}{\varepsilon}\end{aligned}
これを(4)式に代入すると
\begin{aligned}\sigma=\varepsilon_{o}E+\sigma_{p} \\ \sigma_{p}=\sigma \left (1-\dfrac{\varepsilon_{o}}{\varepsilon}\right)\end{aligned}
(2)無限平面誘電体
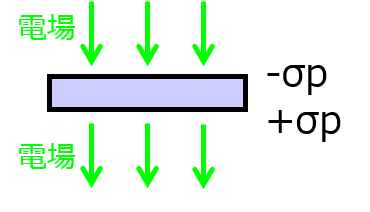
電束密度\(D\)について、真空中と誘電体中とで連続である。
\begin{aligned}D=\varepsilon_{o}E_{o}=\varepsilon E \end{aligned}
これを変形して
\begin{aligned}E=\dfrac{\varepsilon_{o}}{\varepsilon}E_{o}\end{aligned}
\(P=\sigma_{p}\)より、以上の内容を(4)式に代入して
\begin{aligned}\sigma_{p}&=\varepsilon_{o}(E_{o}-E) \\ &=\dfrac{\varepsilon_{o}}{\varepsilon}(\varepsilon-\varepsilon_{o})E_{o}\end{aligned}
(3)外部電場が平行にかかる場合
外部電場に誘起されて誘電分極は発生しないため、\(P=0\)
よって、分極電荷の面密度も0。
(4)誘電体中の導体球
電束密度\(D\)によるガウスの法則を考える。半径r>aの球を取ると、求める電束密度は
\begin{aligned}D=\dfrac{Q}{4 \pi r^{2}}\end{aligned}
これより、誘電体中の電場は、\(D=\varepsilon E\)より
\begin{aligned}E=\dfrac{Q}{4 \pi \varepsilon r^{2}}\end{aligned}
次に、誘電体と導体球との境界に現れる分極電荷を考える。r=aの範囲でガウスの法則を考えると、真電荷と分極電荷の影響を両方考えることができるため
\begin{aligned}E=\dfrac{Q+Q_{p}}{4 \pi a^{2} \varepsilon_{o}}\end{aligned}
(14)式にr=aを代入し、(15)式に適用すると、求める分極電荷の量は
\begin{aligned}Q_{p}=\left(\dfrac{\varepsilon_{o}}{\varepsilon}-1 \right)Q\end{aligned}
最後に
分極電荷が発生する因果関係が分かっていないと、立式する際に誘電率\(\varepsilon_{o},\varepsilon\)の区別が付かずに苦戦することがあります。
是非、自分なりのイメージを付けて、迷いなく立式できるようにしましょう。