 数学
数学 固有ベクトルを用いた行列のn乗の計算
本問は、固有値の性質を利用し、\(A^{n}\)の乗数を落としていき、結果を求める問題です。色々な大学でたまに出題されます。(電通大2023など)まず自力で解けるか確認し、分からなかった場合は復習に役立てて下さると幸いです。
 数学
数学 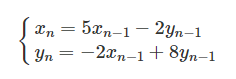 数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学  数学
数学