 量子・電子物性
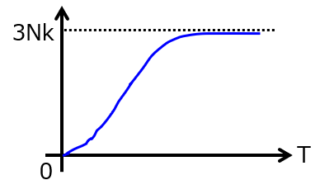
量子・電子物性 デュロン・プティの法則と温度に対する格子比熱の依存性
今までの比熱の式は、指数関数の累乗で表されており、難解なものでした。一方で、高温環境下ではモル分子とボルツマン係数の積で表されることが分かります。これをデュロン・プティの法則と言います。
 量子・電子物性
量子・電子物性 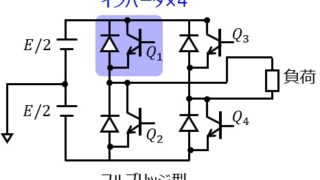 電気回路
電気回路 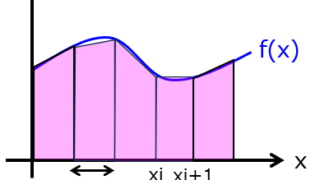 情報
情報 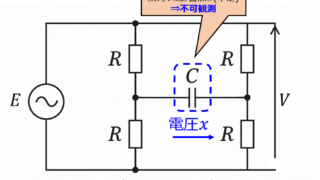 制御工学
制御工学  量子・電子物性
量子・電子物性 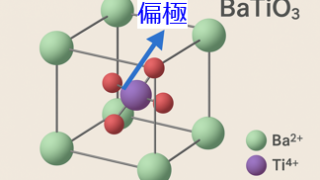 量子・電子物性
量子・電子物性 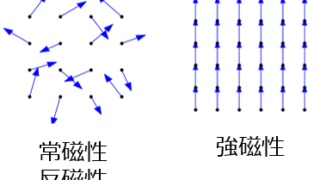 量子・電子物性
量子・電子物性  電磁気学
電磁気学 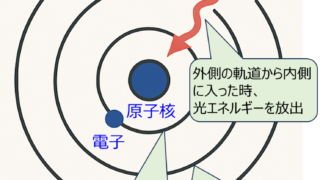 量子・電子物性
量子・電子物性 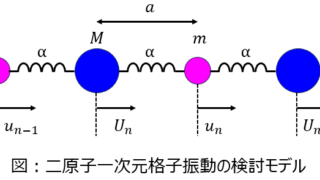 量子・電子物性
量子・電子物性