 電子回路
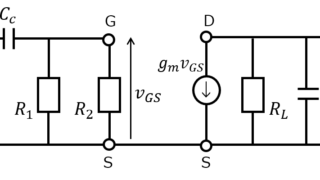
電子回路 【MOSFET】ソース接地RC増幅回路の利得、周波数特性
\(\omega=0\)のとき、分母の\(\omega_{2}\)に関わる項が発散し、∞になります。分子は有限な値なので、利得は0になります。ここから\(\omega\)を大きくしていくと、やがて\(\omega_{2}\)の項が有限な値になります。すると、利得も0より大きい値となるため、上昇傾向になることがわかります。
 電子回路
電子回路 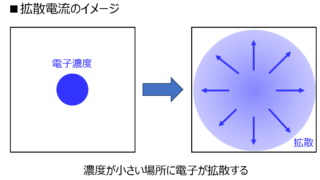 半導体デバイス
半導体デバイス 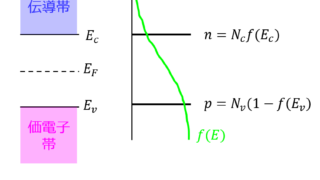 半導体デバイス
半導体デバイス 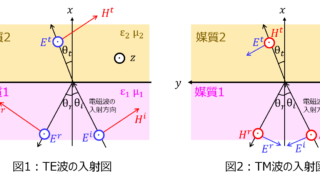 通信
通信 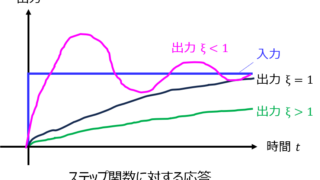 制御工学
制御工学 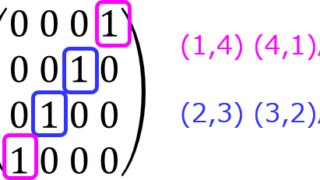 数学
数学  数学
数学  制御工学
制御工学  制御工学
制御工学 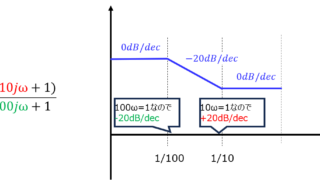 制御工学
制御工学