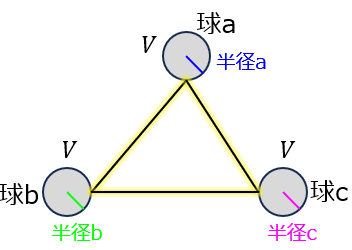
(1)下記の図1のように、半径\(a,b,c\)の球a,b,cが存在する。それぞれの導体の電位が\(V_{a},V_{b},V_{c}\)で、導体同士を導線で接続する。接続後の共通電位、導体ごとの電荷量を求めよ。
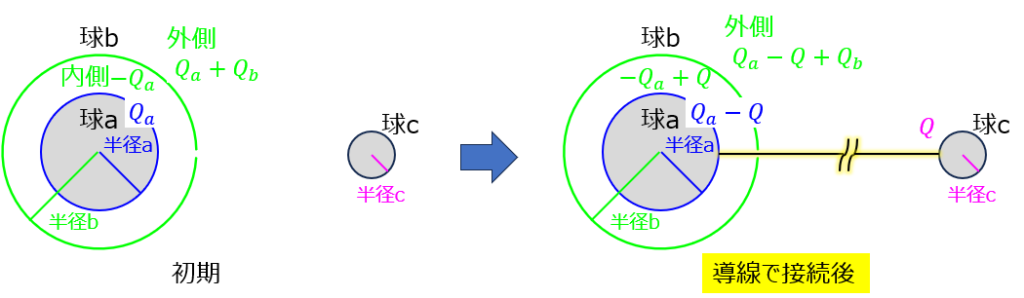
(2)半径\(a,b\)の同心球殻コンデンサが存在する。それぞれに電荷\(Q_{a},Q_{b}\)を与え、外球の小穴を通して遠く離れた初期電荷0の半径\(c\)の球と接続する。半径\(c\)の球に誘起する電荷量\(Q\)を求めよ。
(1)の図
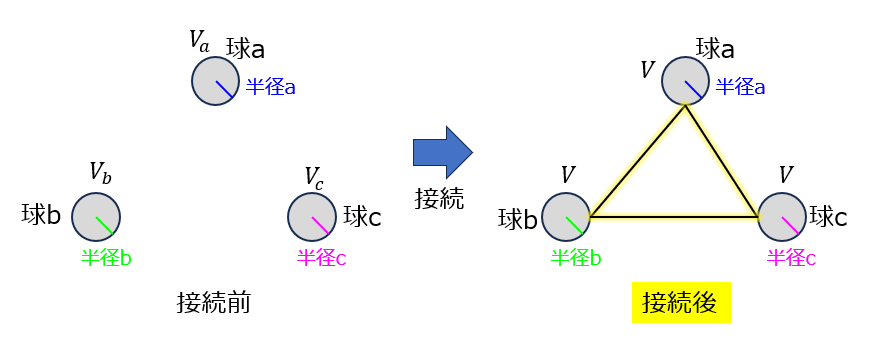
(2)の図
はじめに
本問は、九大で出題されたことがあります。以前の記事では、同心球殻コンデンサの中で接地などの操作をしたときの電荷分布を考えました。本記事では、発展版として、離れた系に存在する導体同士を接続したときの電荷の移動を考えます。
基本事項は変わりません。接続した導体同士の電位は等しいことを念頭に解いていきます。また、本問の条件でにおいて導体は接地していませんので、接続前後で総電荷量は変わらないことにも注目します。
また、無限遠の電位を基準とすると、電位\(V\)、電荷\(Q\)、半径\(r\)の球で起こる関係式は
\begin{aligned}V=\dfrac{Q}{4 \pi \varepsilon_{o} r}\end{aligned}
になります。高校物理でも紹介される式のため詳しい導出は省略しますが、本関係も用います。
解答例
(1)3つの導体を接続したときの電荷分布

まず、接続前の導体で発生する関係式を求めます。(1)式を各球a,b,cに適用すると
\begin{cases}Q_{a}=4 \pi \varepsilon_{o}aV_{a} \\Q_{b}=4 \pi \varepsilon_{o}bV_{b} \\ Q_{c}=4 \pi \varepsilon_{o}cV_{c}\end{cases}
よって、全電荷量\(Q_{all}\)は
\begin{aligned}Q_{all}=4 \pi \varepsilon_{o}(aV_{a}+bV_{b}+cV_{c})\end{aligned}
接続後の各導体における電荷を\(Q’_{a},Q’_{b},Q’_{c}\)とする。全て共通の電位\(V\)となるので
\begin{cases}Q’_{a}=4 \pi \varepsilon_{o}aV \\ Q’_{b}=4 \pi \varepsilon_{o}bV \\ Q’_{c}=4 \pi \varepsilon_{o}cV\end{cases}
接続後の全電荷量\(Q’_{all}\)は
\begin{aligned}Q’_{all}=4 \pi \varepsilon_{o}(a+b+c)V\end{aligned}
これが(3)式と等しいので
\begin{aligned}(aV_{a}+bV_{b}+cV_{c})=(a+b+c)V\end{aligned}
\begin{aligned}V=\dfrac{aV_{a}+bV_{b}+cV_{c}}{a+b+c}\end{aligned}
\(V\)が求まったので、それぞれの導体の電荷量は
\begin{cases}Q’_{a}=\dfrac{4 \pi \varepsilon_{o}a(aV_{a}+bV_{b}+cV_{c})}{a+b+c} \\ Q’_{b}=\dfrac{4 \pi \varepsilon_{o}b(aV_{a}+bV_{b}+cV_{c})}{a+b+c} \\ Q’_{c}=\dfrac{4 \pi \varepsilon_{o}c(aV_{a}+bV_{b}+cV_{c})}{a+b+c} \end{cases}
(2)遠く離れた球に誘起する電荷量

接続後、球aから球cに電荷\(Q\)が移動したとする。球aの電位を\(V_{a}\)とする。電位の基準点を無限遠に取ると
\begin{aligned}V_{a}&=-\int^{b}_{\infty}\dfrac{Q_{a}-Q+Q_{b}}{4 \pi \varepsilon_{o} r^{2}}dr-\int^{a}_{b}\dfrac{Q_{a}-Q}{4 \pi \varepsilon_{o} r^{2}}dr \\ &=\dfrac{Q_{a}-Q+Q_{b}}{4 \pi \varepsilon_{o}b}+\dfrac{Q_{a}-Q}{4 \pi \varepsilon_{o}}\left(\dfrac{1}{a}-\dfrac{1}{b}\right) \end{aligned}
一方で、球cの電位\(V_{c}\)は(1)式により
\begin{aligned}V_{c}=\dfrac{Q}{4 \pi \varepsilon_{o} c}\end{aligned}
上記と(9)式が等しいので
\begin{aligned}\dfrac{Q_{a}-Q+Q_{b}}{b}+(Q_{a}-Q)\left (\dfrac{1}{a}-\dfrac{1}{b}\right)=\dfrac{Q}{c} \end{aligned}
\begin{aligned} \left(\dfrac{1}{a}+\dfrac{1}{c}\right)Q=\dfrac{Q_{1}}{a}+\dfrac{Q_{b}}{b}\end{aligned}
\begin{aligned}Q=\dfrac{\dfrac{Q_{a}}{a}+\dfrac{Q_{b}}{b}}{\dfrac{1}{a}+\dfrac{1}{c}}\end{aligned}
最後に
見慣れない問題かもしれませんが、原理原則から基づいて丁寧に考えていくことで必ず解答できます。本問に限らず、見慣れない問題が出てきても原理原則から考えていく癖を付けていきましょう。