 電磁気学
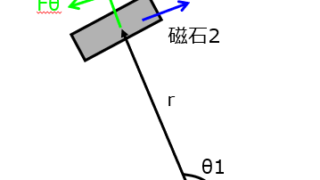
電磁気学 磁石同士に働く力と位置エネルギーの計算問題
外部磁界の磁界の中に磁気モーメントを置いた時の位置エネルギーは、磁気モーメントと外部磁界の内積の負の成分に等しいです。磁気モーメントは、負の磁荷から正の磁荷へ伸びるベクトルのため、無限遠から近づけていくとき、外部磁場との引力が発生します。これを相殺することから、負になる。ということですね。
 電磁気学
電磁気学 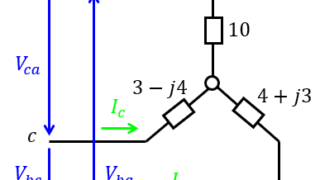 電気回路
電気回路  電気回路
電気回路 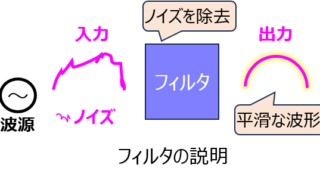 電気回路
電気回路 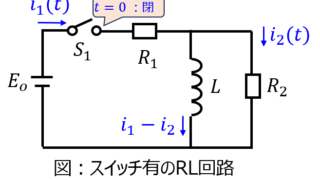 電気回路
電気回路 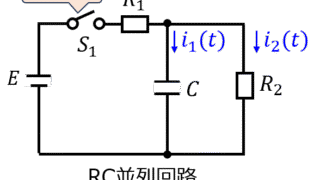 電気回路
電気回路 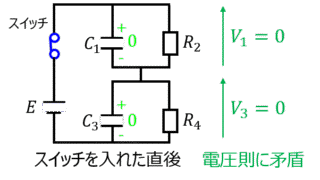 電気回路
電気回路 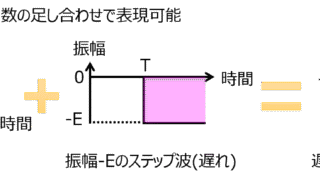 電気回路
電気回路  電気回路
電気回路  電気回路
電気回路