 電磁気学
電磁気学 【電磁気学】ラプラス方程式を利用した電位の計算問題
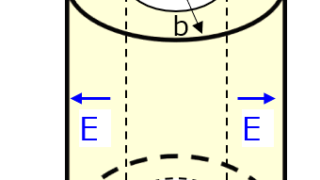
電位の空間的な分布と電荷の分布を表しています。解答に際してpn接合半導体でも同じでしたが、変数分離法を用いて微分方程式を解くことに帰着します。例えば、(1)式はラプラシアン\(\Delta\)が含まれているため、2階微分項になっています。このため、2回積分をすると電位が求まり、1回だけの積分でも¥(E=-gradV¥)より、電場が求まります。
 電磁気学
電磁気学  コラム
コラム 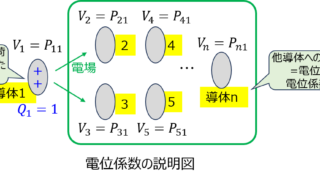 電磁気学
電磁気学 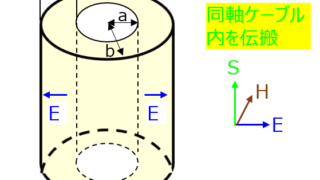 電磁気学
電磁気学 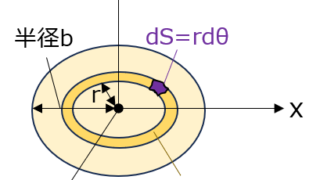 電磁気学
電磁気学 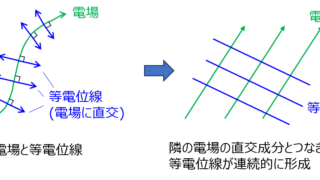 電磁気学
電磁気学 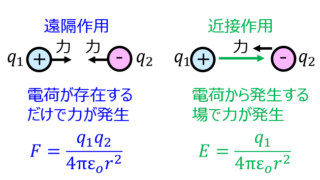 電磁気学
電磁気学 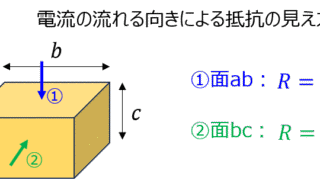 電磁気学
電磁気学 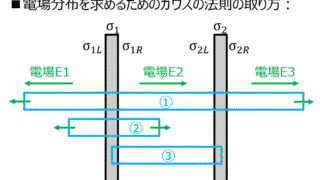 電磁気学
電磁気学 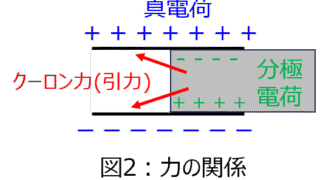 電磁気学
電磁気学